质因数2或5是什么意思（质因数都是几）

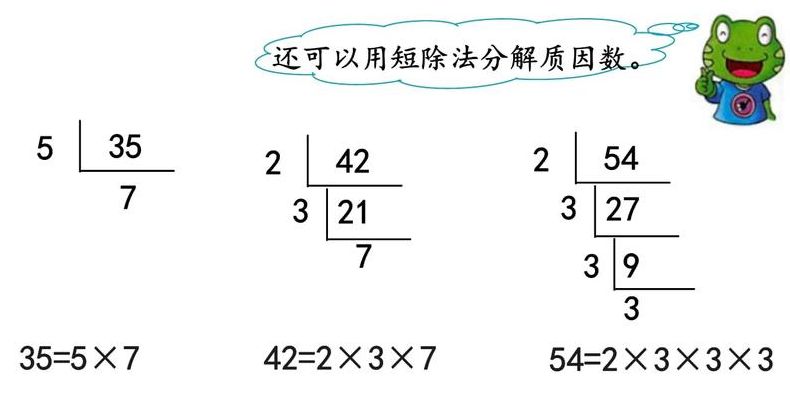
质因数是什么意思

质因数（素因数或质因子）在数论里是指能整除给定正整数的质数。质因数（素因数或质因子）在数论里是指能整除给定正整数的质数。除了1以外，两个没有其他共同质因子的正整数称为互质。因为1没有质因子，1与任何正整数（包括1本身）都是互质。

质因数（素因数或质因子）在数论里是指能整除给定正整数的质数。除了1以外，两个没有其他共同质因子的正整数称为互质。因为1没有质因子，1与任何正整数（包括1本身）都是互质。简单说就是：一个整数，它有若干个因数，其中一个因数是素数，（这个因数除了1和它自己外没有别的因数了。

质因数是指在数论中，素数因子（素数因子或素数因子）是指将给定的正整数相除的素数。除1外，没有其他公共素数因子的两个正整数称为倒数素数。因为1没有素数因子，所以1和任何正整数（包括1本身）都是素数。

质因数是能够整除给定数字的质数。换句话说，质因数是一个自然数，除了1和它自身以外，无法被其他自然数整除的数。详细解释如下：质数的概念 质数是一个大于1的自然数，它只有两个正因数：1和它本身。例如，7等都是质数。

质因数（素因数或质因子）是数论中的概念，指的是能够整除给定正整数的质数。 两个正整数如果没有除了1以外的共同质因数，则它们被称为互质。 1没有质因子，因此它与任何正整数（包括自身）都是互质的。

质因数就是一个数的约数，并且是质数，比如8=2×2×2，2就是8的质因数。12=2×2×3，2和3就是12的质因数。把一个式子以12=2×2×3的形式表示，叫做分解质因数。16=2×2×2×2，2就是16的质因数，把一个合数写成几个质数相乘的形式表示，这也是分解质因数。

为什么分解质因数是分母是2或5的数就是整数不是2和5数就是循环小数

因为2， 5都是10的因子，2的n次方，5的n次方至少会被10的n次方整除。因此在分母上只有2或5的因子时，总会被十分位，百分位，千分位，.中的某个约掉，也就不会循环了。其它质因数都约不掉，只能循环。

最简分数，如果分母中只含有2和5的质因数，不含有其他质因数，这个分数就能化成有限小数。如果一个最简分数的分母中含有2和5以外的质因数，这个分数就不能化成有限小数.一个不能化成有限小数的最简分数，必然可以化成无限循环小数。这时，先把这个分数的分母分解质因数。

①一个最简分数，如果分母中既含有质因数2和5，又含有2和5以外的质因数，那么这个分数化成的小数必定是混循环小数。②一个最简分数，如果分母中只含有2和5以外的质因数，那么这个分数化成的小数必定是纯循环小数。

分数是最简分数的话，那么如果分母的质因数只有2和5的话，就能化成有限小数，如果分母的质因数有2和5以外的质数的话，就只能化成无限小数，不是最简分数，先约分再判断。

先利用分解质因数的方法，把分子和分母进行约分，化成最简分数。此时如果分母的质因数只有2或5，那么商一定是有限小数。如果还包含了其他因数，那么商一定是无限循环小数。

解决这个问题，首先运用分类的思想，排除公认的部分，只需说明其余部分即可。有理数是整数和分数的总称。整数，公认的当然不是无限小数。下面说明分数，可以把它分为两类。第一类，约分后，分母只含有2或5的质因数，这类分数化为小数后，一定是有限小数。

能分数化小数最简分数的分母分解质因数只能含2和5是什么意思?

1、如果一个最简分数的分母分解质因数后，只含有2和5，那么这个最简分数就可以化为有限小数。而且，有限小数的位数等于分母分解质因数后2或5多的那个数的个数。如果分母中含有2和5以外的其它质数，就不能化为有限小数。如：因为11/8的分母8=2×2×2，只含有2，所以11/8可化为有限小数。

2、最简分数，如果分母中只含有2和5的质因数，不含有其他质因数，这个分数就能化成有限小数。如果一个最简分数的分母中含有2和5以外的质因数，这个分数就不能化成有限小数.一个不能化成有限小数的最简分数，必然可以化成无限循环小数。这时，先把这个分数的分母分解质因数。

3、分数是最简分数的话，那么如果分母的质因数只有2和5的话，就能化成有限小数，如果分母的质因数有2和5以外的质数的话，就只能化成无限小数，不是最简分数，先约分再判断。

4、一个最简分数，如果把分母分解质因数，质因数中如果不含有2和5以外的质数，这个分数就可以化成有限小数，否则就不能化成有限小数。圆周率π圆的周长与直径的比值，是一个定值，和圆的大小无关。

只含质因数2或5是什么意思

1、如果一个最简分数的分母分解质因数后，只含有2和5，那么这个最简分数就可以化为有限小数。而且，有限小数的位数等于分母分解质因数后2或5多的那个数的个数。如果分母中含有2和5以外的其它质数，就不能化为有限小数。如：因为11/8的分母8=2×2×2，只含有2，所以11/8可化为有限小数。

2、因为 1/2=0.5 ， 1/5=0.2 ，当最简分数的分母中只含有质因数2，5时（当然是有限个），它均可以写成有限个0.5和有限个0.2的乘积，所以，它的小数位数最终必定是有限的，所以，能够化成有限小数。

3、因为分母中只要含有质因数5的分数都能化成十进分数，十进分数都能化成有限小数；如果还含有其他质因数，则不能化成十进分数，就不能化成有限小数.不是说任何数都能被数整除，但可以被10整除，如M /10=0.1M ，当最简分数的分母中只要含有质因数2，5时，可以看作是关于除以了10的倍数的问题。

4、商是循环小数，又分两种情况：如果除数只含有2和5以外的质因数，那么，其商就是纯循环小数；如果除数既含有质因数2或5，又含有2和5以外的质因数，那么，其商就是混循环小数。例如，37÷148÷265÷50=13÷10的除数只含有质因数5，它们的商都是有限小数。

5、不对。正确的说法是∶在一个最简分数中，分母中只含有质因数2或或者是2和5的分数，才能化成有限小数。如∶1/15，把分母分解质因数得：15＝3×5，虽然它含有质因数5，但，它还有一个质因数3，因此，1/15不能化成有限小数。

什么是质因数举例说明

质因数定义 质因数（或称质数）是指一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数。例如，7等都是质数。 质因数举例说明 - 2是最小的质数，它也是唯一的偶数质数。- 3是质数，它只有1和3两个因数。- 4不是质数，因为4除了能被1和4整除外，还能被2整除。

定义质因数：一个自然数的因数中，如果能够整除该数的质数被称为这个数的质因数。 质因数示例：例如，对于数字24，其因数包括12和24。在这些因数中，2和3是质数，因此它们是24的质因数。 分解质因数：将一个合数表示为质因数相乘的形式称为分解质因数。

在数论里是指能整除给定正整数的质数。除了1以外，两个没有其他共同质因子的正整数称为互质。因为1没有质因子，1与任何正整数（包括1本身）都是互质。正整数的因数分解可将正整数表示为一连串的质因子相乘，质因子如重复可以用指数表示。

质因数，就是指一个正整数的约数，并且该数还属于是质数的数字，质因数有时候也被我们叫做“素因数”和“质因子”，举例子来说，在2×2×2=8这个等式当中，数字2是数字8的约数，且2还属于质数，就称2是8的质因数。

质因数（素因数或质因子）在数论里是指能整除给定正整数的质数。除了1以外，两个没有其他共同质因子的正整数称为互质。因为1没有质因子，1与任何正整数（包括1本身）都是互质。正整数的因数分解可将正整数表示为一连串的质因子相乘，质因子如重复可以用指数表示。

举例说明，以数字12为例，它能被4个自然数整除，即和4，所以12不是素数。而11则不能被小于它的任何自然数整除，因此11为素数。总的来说，质因数和质数是数论中的基础概念，理解它们对于深入学习数学有着至关重要的作用。通过将合数分解为质数的乘积，我们能够更好地理解数的结构和性质。

The End