帕斯卡三角形（帕斯卡三角形内角和）

数学家帕斯卡的故事

1、帕斯卡(1623-1662)，法国数学家、物理学家、近代概率论的奠基者。他提出一个关于液体压力的定律，后人称为帕斯卡定律。他建立的直觉主义原则对于后来一些哲学家，如卢梭和伯格森等都有影响。

2、帕斯卡尔（BlaisePascal）是一位法国数学家、物理学家和哲学家，他在数学和物理学领域做出了许多杰出的贡献。他的成就包括发明了第一台计算器、发现了帕斯卡三角形、研究了气体压力等。

3、帕斯卡生于法国奥弗涅的克莱蒙费朗，从小他就智力高人一等，聪明伶俐，12岁时就爱上数学，数学的魔力让这个孩子几乎废寝忘食。

帕斯卡三角形有哪些美妙的规律呢

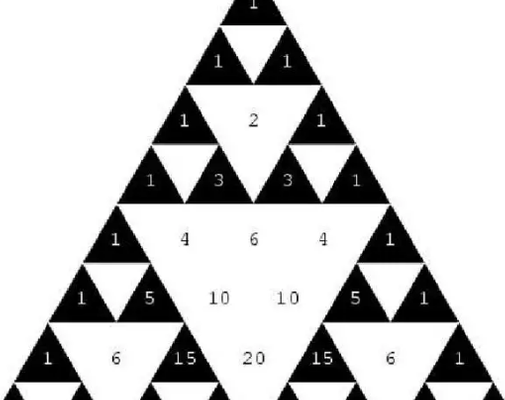
1、每个数等于它上方两数之和。每行数字左右对称，由1开始逐渐变大。第n行的数字有n项。第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。

2、帕斯卡三角形还与二项式定理和组合数有密切关系，对于展开式 (a + b)^n 的系数就对应着第 n 行的数字。

3、莱洛三角形的斜边长度也是一个整数。 莱洛三角形的面积是一个整数。 莱洛三角形的周长是一个整数。 莱洛三角形的高也是一个整数。这些特点使得莱洛三角形在几何学和数论中都具有一定的重要性和研究价值。

什么是帕斯卡三角形?她怎么算事物的可能性?

1、帕斯卡三角在中国叫杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，叫做帕斯卡三角形。帕斯卡是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。

2、贾宪三角（贾宪三角）一般指杨辉三角，杨辉三角，是二项式系数在三角形中的一种几何排列。在欧洲，这个表叫做帕斯卡三角形。帕斯卡（1623---1662）是在1654年发现这一规律的，比杨辉要迟393年，比贾宪迟600年。

3、第n行的第m个数和第n-m+1个数相等 ，为组合数性质之一。每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。

4、*...*2*1)杨辉三角，是二项式系数在三角形中的一种几何排列，在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲，帕斯卡（1623---1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。

5、帕斯卡三角形除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和，形似三角形，在中国首现于南宋杨辉的《详解九章算法》得名，书中杨辉说明是引自贾宪的《释锁算书》，故又名贾宪三角形。

帕斯卡三角的性质是什么?

性质：每行数字左右对称，由1开始逐渐变大，然后变小，回到1。第n行的数字个数为n个。第n行数字和为2^(n－1)。每个数字等于上一行的左右两个数字之和。可用此性质写出整个帕斯卡三角形。

帕斯卡三角形即杨辉三角，二项式系数在三角形中的一种几何排列。

“帕斯卡三角”中数的排列规律是：每一行两端都是1，其余各数都是上一行中与比数最相邻的两数之和。

The End