梯形中位线（梯形中位线公式）

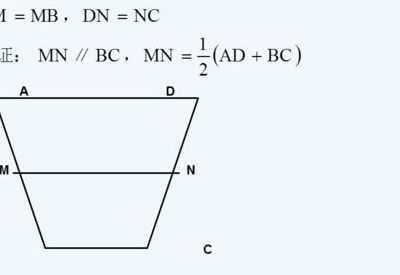
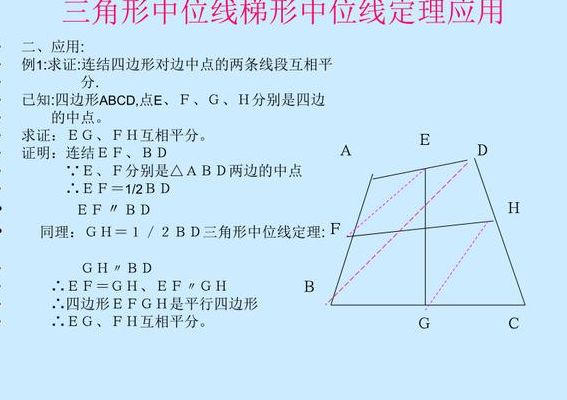
梯形中位线定理

梯形中位线定理是梯形几何性质中的一个定理，它表明梯形的两条对角线的中点连线是平行于梯形的底边，并且中位线的长度等于梯形两个底边长度之和的一半。

梯形中位线定理是几何学的一个定理，是指连接梯形两腰中点的线段叫做梯形的中位线，梯形的中位线平行于两底，并且等于两底和的一半。定理定义 梯形的中位线等于梯形的上底加下底再除以二，用符号表示是L。

连接梯形两腰中点的线段叫做梯形的中位线，梯形的中位线平行于两底，并且等于两底和的一半。

梯形中位线定理 连接梯形两腰中点的线段叫做梯形的中位线，梯形的中位线平行于两底，并且等于两底和的一半。梯形的中位线L平行于底边，且其长度为上底加下底和的一半，用符号表示是：L=(a+b)/2。

梯形的中位线定理是指连接梯形两腰中点的线段叫做梯形的中位线，梯形的中位线平行于两底，并且等于两底和的一半，连结梯形两腰中点的线段就是梯形的中位线。

中位线定理：(1)三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半。(2)梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半。图的话，打开下面的网址就可以了。

梯形中位线公式

1、梯形中位线公式：中位线=(上底+下底)/2。扩展知识 关于中位线 中位线是一个数学术语，是平面几何内的三角形任意两边中点的连线或梯形两腰中点的连线。三角形：连接三角形两边中点的线段叫做三角形的中位线。

2、梯形中位线定理是L=（a+b）/2。梯形中位线定理是梯形的一个重要性质，在初中几何教学中占有重要地位。它既是对三角形中位线定理的拓展与应用。又为今后有关两条线平行和线段倍分关系的证明与应用提供了更为可行的方法。

3、求梯形中位线公式：EF=(AD+BC)/2。中位线是一个数学术语，是平面几何内的三角形任意两边中点的连线或梯形两腰中点的连线。

直角梯形中位线定理

直角梯形中点连线性质直角梯形的中位线平行于两底，等于两底和的一半，垂直于一条腰。相关信息 性质的内容是梯形的中位线平行于两底，并且等于两底和的一半 。

梯形中位线定理是几何学的一个定理，是指连接梯形两腰中点的线段叫做梯形的中位线，梯形的中位线平行于两底，并且等于两底和的一半 。常用辅助线 作高（根据实际题目确定）。平移一腰。平移对角线。

梯形中位线定理是L=（a+b）/2。梯形中位线定理是梯形的一个重要性质，在初中几何教学中占有重要地位。它既是对三角形中位线定理的拓展与应用。又为今后有关两条线平行和线段倍分关系的证明与应用提供了更为可行的方法。

面积公式：梯形中位线×高=（上底+下底）×高÷2=梯形面积。梯形中位线到上下底的距离相等。中位线长度=（上底+下底）÷2。相关误区 梯形的中位线是连结两腰中点的线段而不是连结两底中点的线段。

梯形的中位线定理是连接梯形两腰中点的线段叫做梯形的中位线，梯形的中位线平行于两底，并且等于两底和的一半。梯形的面积公式：（上底+下底）×高÷2 梯形的面积等于上下两底之和与高的乘积的一半。

梯形的中位线有什么性质?

梯形中位线的性质：梯形的中位线平行于两底，并且等于两底和的一半。梯形中位线的2倍乘高再除以二就等于梯形的面积，用符号表示是L。中位线在关于梯形的各种题型中都是一条得天独厚的辅助线。

梯形中位线定理是几何学的一个定理，是指连接梯形两腰中点的线段叫做梯形的中位线。性质是：梯形的中位线平行于两底，并且等于两底和的一半。梯形中位线定理是梯形的一个重要性质，在初中几何教学中占有重要地位。

梯形中位线性质：梯形的中位线平行于两底，并且等于两底和的一半。梯形中位线的2倍乘高再除以二就等于梯形的面积，用符号表示是L。中位线是一个数学术语，至平面几何内的三角形任意两边中点的连线或梯形两腰中点的连线。

梯形中位线定理是梯形的一个重要性质，既是对三角形中位线定理的拓展与应用，又为今后有关两条线平行和线段倍分关系的证明与应用提供了更为可行的方法，中位线是在三角形或梯形中一条特殊的线段。

性质的内容：（1）梯形的中位线平行于两底，并且等于两底和的一半 。（2）梯形中位线的2倍乘高再除以二就等于梯形的面积，用符号表示是L。

The End