大学物理高斯定理（大学物理高斯定理表达式）

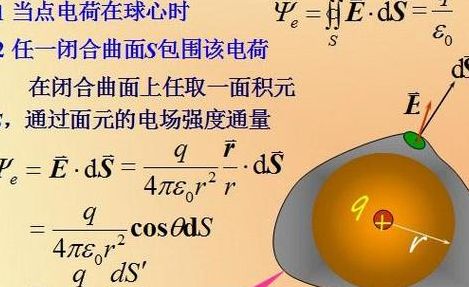
大学物理关于高斯定理

1、高斯定理，又称为高斯通量定理，是物理学中的一个基本定理，描述了电场或磁场通过某一闭合曲面的总通量与该闭合曲面内的电荷或磁荷之间的关系。

2、是一个重要的积分公式。高斯定理：矢量穿过任意闭合曲面的通量等于矢量的散度对闭合面所包围的体积的积分。它给出了闭曲面积分和相应体积分的积分变换关系，是矢量分析中的重要恒等式。是研究场的重要公式之一。

3、高斯定理数学公式是∮F·dS=∫(▽·F)dV。高斯定律显示了封闭表面的电荷分布和产生的电场之间的关系。设空是有界闭区域ω，其边界ω是分段光滑闭曲面。函数P(x，y，z)，Q(x，y，z)。

4、高斯定理反映的是 电场强度E对闭合曲面的积分与曲面内包含电荷量的关系，所以是二重积分。

5、电场中的高斯定理表明静电场是有源场；定理数学表达式的等号右边不等于零； 电场中的高斯定理还常常用来求具有对称性的带电体所产生的电场。而磁场中的高斯定理表明稳恒电场是无源场；定理数学表达式的等号右边等于零。

6、大学物理中所处理的带电体多半不能看成点电荷，求电场的方法有：1．利用点电荷Q的场强公式E＝kQ／r＾2，将连续带电体分割成电荷元dq，然后用积分计算带电体的场强。

大学物理高斯定理公式

是一个重要的积分公式。高斯定理：矢量穿过任意闭合曲面的通量等于矢量的散度对闭合面所包围的体积的积分。它给出了闭曲面积分和相应体积分的积分变换关系，是矢量分析中的重要恒等式。是研究场的重要公式之一。

ρ---电荷的体密度 dV---体积元 ρdV---所取 体积元 的带电量 ∫ρdV ---就是 高斯面内 的 总电荷量。

高斯定理是：电通量=任何的闭合曲面包围的净电荷除以介电常数，这个定理中的“闭合曲面”就叫高斯面。在球面内做一个高斯面，其所包围的净电荷为零，根据高斯定理，球面内场强处处为零。

由 既P点的电场强度改变.由 既整个过程穿过S面的电通量不变。

中文名称：高斯定理 英文名称：Gauss theorem 定义：通过任意闭合曲面的电通量等于该闭合曲面所包围的所有电荷量的代数和与电常数之比。

公式为： ∮F·dS=∫▽·Fdv ▽是哈密顿算符 F、S为矢量 高斯定理在物理学研究方面，应用非常广泛。

简述真空中的高斯定理

高斯定律：在静电场中，穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷的代数和有关，且等于封闭曲面的电荷的代数和除以真空中的电容率。表明在闭合曲面内的电荷分布与产生的电场之间的关系。

根据静电场的高斯定理：静电场的电场线起于正电荷或无穷远，终止于负电荷或无穷远，故静电场是有源场。从安培环路定理来说它是一个无旋场。

它表示，电场强度对任意封闭曲面的通量只取决于该封闭曲面内电荷的代数和，与曲面内电荷的位置分布情况无关，与封闭曲面外的电荷亦无关。在真空的情况下，Σq为包围在封闭曲面内的自由电荷的代数和。

高斯定理：通过任何一个闭合曲面的电通量，等于这个曲面所包围的净电荷与真空中的介电常数的比值，即∮E·dS=Q/ε0 对于电荷的分布有对称性的情形，如果选择恰当的高斯面，用高斯定理求电场常常比较方便。

真空中高斯定律积分形式为：如果对于一个闭合曲面，定义向外为正法线的指向，则进入曲面的磁通量为负，出来的磁通量为正，那么就可以得到通过一个闭合曲面的总磁通量为0。

有什么简单易懂的方法理解大学物理里面的高斯面与高斯定理?_百度...

1、解释：高斯面是高斯定理中的任一闭合曲面，指真空中的任何静电场中，穿过任一闭合曲面的电通量，在数值上等于该闭合曲面内包围的电量的代数和乘以1/ε。

2、高斯定理：通过任何一个闭合曲面的电通量，等于这个曲面所包围的净电荷与真空中的介电常数的比值，即∮E·dS=Q/ε0 对于电荷的分布有对称性的情形，如果选择恰当的高斯面，用高斯定理求电场常常比较方便。

3、例如，可以用高斯定理来证明库仑定律，即两个静电荷之间的电力与它们之间的距离的平方成反比。此外，还可以用高斯定理来推导出电场的其他基本概念，如电通量密度和电势能等。

4、那怎么证明E是常量，把E提出积分外？E等于0啊，就是常量。我的疑惑就是不知道为什么高斯面上每一点的场强大小相等，不要只说什么对称性，我希望能说的详细清楚点。

The End