什么叫数轴（什么叫数轴?数轴的三要素是什么?）

什么叫做数轴

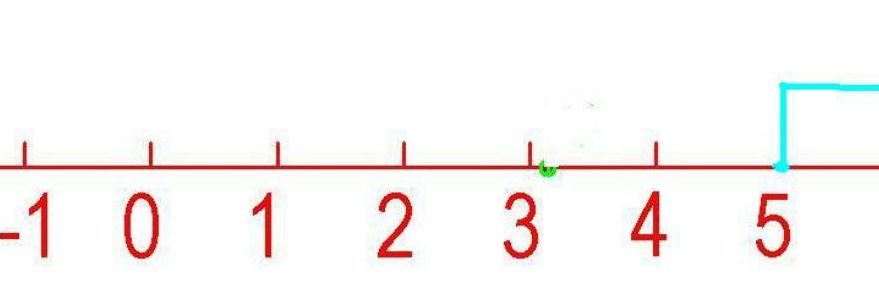
1、什么叫做数轴如下：数轴（number axis），为一种特定几何图形。直线是由无数个点组成的集合，实数包括正实数、零、负实数也有无数个。正因为它们的这个共性，所以用直线上无数个点来表示实数。

2、数轴是数形结合的产物，是指在数学中，用一条直线上的点表示数，并规定了原点、正方向、单位长度的直线。

3、数轴（number axis）规定了原点（origin），正方向和单位长度的直线叫数轴。所有的实数都可以用 数轴上的点来表示。也可以用数轴来比较两个实数的大小。

4、数轴，为一种特定几何图形。直线是由无数个点组成的集合，实数包括正实数、零、负实数也有无数个。正因为它们的这个共性，所以用直线上无数个点来表示实数。原点 数轴上的原点与实数0对应，代表实数0。

什么是数轴?

在数学中，可以用一条直线上的点表示数，这条直线 叫做数轴(number line)，在数学中有着广泛的运用。两根互相垂直且原点重合的数轴可以构成平面直角坐标系；三根互相垂直且原点重合的数轴可以构成空间直角坐标系。

数轴是一个用来表示实数的直线图形，它将实数按照大小顺序进行排列，并将它们与直线上的点一一对应。数轴上的一个点通常被称为一个数，它与数轴上的每个其他点之间都有一个对应关系。

数轴是数形结合的产物，是指在数学中，用一条直线上的点表示数，并规定了原点、正方向、单位长度的直线。

数轴是数学中一种直观、简洁的表示数的工具，广泛地应用于初中、高中和大学的数学教学中。

数轴规定了原点，正方向和单位长度的直线叫数轴。所有的实数都可以用 数轴上的点来表示。也可以用数轴来比较两个实数的大小。

数轴（number axis），为一种特定几何图形。直线是由无数个点组成的集合，实数包括正实数、零、负实数也有无数个。正因为它们的这个共性，所以用直线上无数个点来表示实数。

什么叫数轴定义

数轴定义是指以数轴（也称为实数轴）来定义数的概念和数的关系。数轴是一条直线，上面的每个点都与实数对应。数轴上规定了一个固定的原点（通常表示为0），并且根据确定的刻度将整个数轴分割成等距的部分。

什么是数轴的定义介绍如下：数轴是数学中用来表示实数的直线图形。它是一个直线，上面标记了所有实数，并按照从左到右的顺序排列。数轴上的每个点代表一个实数，而数轴的中点通常表示0。

数轴的定义：规定了原点、正方向和单位长度的直线叫数轴。其中，原点、方向和单位长度称为数轴的三要素。数轴 数轴，为一种特定几何图形。直线是由无数个点组成的集合，实数包括正实数、零、负实数也有无数个。

数轴是数形结合的产物，是指在数学中，用一条直线上的点表示数，并规定了原点、正方向、单位长度的直线。

谁知道什么叫数轴

1、在数学中，可以用一条直线上的点表示数，这条直线 叫做数轴(number line)，在数学中有着广泛的运用。两根互相垂直且原点重合的数轴可以构成平面直角坐标系；三根互相垂直且原点重合的数轴可以构成空间直角坐标系。

2、什么叫做数轴如下：数轴（number axis），为一种特定几何图形。直线是由无数个点组成的集合，实数包括正实数、零、负实数也有无数个。正因为它们的这个共性，所以用直线上无数个点来表示实数。

3、数轴是数形结合的产物，是指在数学中，用一条直线上的点表示数，并规定了原点、正方向、单位长度的直线。

在数学中什么叫数轴

在数学中，可以用一条直线上的点表示数，这条直线 叫做数轴(number line)，在数学中有着广泛的运用。两根互相垂直且原点重合的数轴可以构成平面直角坐标系；三根互相垂直且原点重合的数轴可以构成空间直角坐标系。

数轴（number axis）规定了唯一的原点（origin），唯一的正方向和唯一的单位长度的直线叫数轴。所有的有理数都可以用 数轴上的点来表示。也可以用数轴来比较两个实数的大小。

数轴是数形结合的产物，是指在数学中，用一条直线上的点表示数，并规定了原点、正方向、单位长度的直线。

什么是数轴

1、在数学中，可以用一条直线上的点表示数，这条直线 叫做数轴(number line)，在数学中有着广泛的运用。两根互相垂直且原点重合的数轴可以构成平面直角坐标系；三根互相垂直且原点重合的数轴可以构成空间直角坐标系。

2、什么叫做数轴如下：数轴（number axis），为一种特定几何图形。直线是由无数个点组成的集合，实数包括正实数、零、负实数也有无数个。正因为它们的这个共性，所以用直线上无数个点来表示实数。

3、数轴是一个用来表示实数的直线图形，它将实数按照大小顺序进行排列，并将它们与直线上的点一一对应。数轴上的一个点通常被称为一个数，它与数轴上的每个其他点之间都有一个对应关系。

4、数轴是数形结合的产物，是指在数学中，用一条直线上的点表示数，并规定了原点、正方向、单位长度的直线。

The End