函数拐点（函数拐点是点还是横坐标）

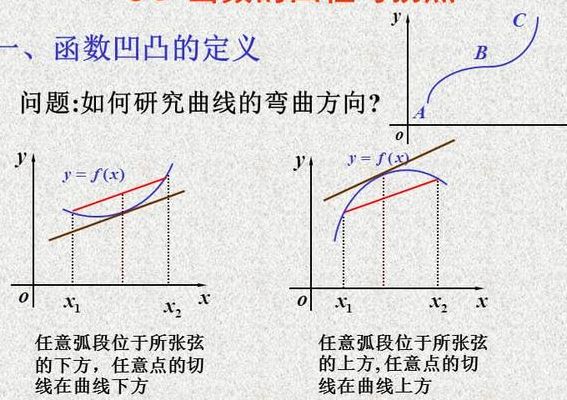
什么是拐点?

1、拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即曲线的凹凸分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。

2、拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。

3、拐点（别称：反曲点）在数学上是指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即曲线的凹凸分界点）。

4、零点，驻点，极值点指的都是函数y=f(x)的一个横坐标x0，而拐点指的是函数y=f(x)图像上的一个点。拐点：二阶导数为零，且三阶导不为零；驻点：一阶导数为零或不存在。

5、拐点原是高等数学中的一个概念，应用到传媒领域，是指中国媒介改革还存在很大的增量空间。但是，如果按照现行的发展模式、发展框架发展下去而不做变革，这种增量空间就很难得到挖掘。

什么是函数的拐点?

函数的拐点是事物发展过程中运行趋势或运行速率的变化，也就是指凸曲线与凹曲线的连接点，当函数图像上的某点使函数的二阶导数为零，且三阶导数不为零时，这点即为函数的拐点。

零点，驻点，极值点指的都是函数y=f(x)的一个横坐标x0，而拐点指的是函数y=f(x)图像上的一个点。拐点：二阶导数为零，且三阶导不为零；驻点：一阶导数为零或不存在。

总函数曲线的拐点是指总函数曲线上的一点，在这点的左侧，总函数曲线以递增的速度的上升，在这点的右侧，总函数曲线以递减的速度上升。当总函数为拐点时，其边际产量为最大值。我们可以依据这个规律求出这个拐点。

拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。

请问怎么求函数的拐点啊?

讨论二阶导数，对定义域内每一个二阶导的实根或二阶导数不存在的点x，检查其左右两侧符号，当两侧符号相反时，即为拐点。讨论三阶导数，若在x的邻域内二阶导为0而三阶导不为0则必为函数拐点。

求两次导，另二阶导等于，得对称中心。三次函数的拐点就是三次函数的对称中心 拐点求法：设三次函数 y=f(x)=ax^3+bx^2+cx+d，a不为0。则y=3ax^2+2bx+c。y=6ax+2b。由a不为0。

求拐点的方法如下：拐点和极值点通常是不一样的，两者的定义是不同的。极值点处一阶导数为0，一阶导数描述的是原函数的增减性。拐点处二阶导数为0，二阶导数描述的是原函数的凹凸性。判读方法不同。

x)的极值点。拐点在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即曲线的凹凸分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。

拐点 是事物发展过程中运行趋势或运行速率的变化。在数学领域是指，凸曲线与凹曲线的连接点！当函数图像上的某点使函数的二阶导数为零，且三阶导数不为零时，这点即为函数的拐点。

若函数y=f(x)在c点可导，且在点c一侧是凸，另一侧是凹，则称c是函数y=f(x)的拐点。

如何判断函数的拐点?

1、②求出函数二阶导。③求拐点，令二阶导数等于0，在二阶导数零点处右极限异号。④二阶导数大于0，凹区间，反之凸区间。

2、然后，判断驻点两侧的函数值符号是否相反。如果驻点两侧的函数值符号相反，那么这个驻点很可能是拐点。 接下来，求出函数的二阶导数（f(x)）。二阶导数表示函数曲线的凹凸性。

3、方法：（1）求这个函数的二阶导数；（2）若二阶导数在这个点的左边和右边的正负性不同，则这个点就是拐点；若在这个点的左边和右边的正负性相同，则这个点就不是拐点。

如何求函数的拐点?

1、方法：（1）求这个函数的二阶导数；（2）若二阶导数在这个点的左边和右边的正负性不同，则这个点就是拐点；若在这个点的左边和右边的正负性相同，则这个点就不是拐点。

2、拐点求法：y=f(x）的拐点：求f(x）；令f(x)=0，解出方程的实根，求出在区间I内f(x）。拐点和极值点通常是不一样的，两者的定义是不同的。极值点处一阶导数为0，一阶导数描述的是原函数的增减性。

3、若函数y=f(x)在c点可导，且在点c一侧是凸，另一侧是凹，则称c是函数y=f(x)的拐点。我们可以按下列步骤来判断区间I上的连续曲线y=f(x)的拐点：（1）求f(x)。

怎么判断函数的拐点呢?

1、②求出函数二阶导。③求拐点，令二阶导数等于0，在二阶导数零点处右极限异号。④二阶导数大于0，凹区间，反之凸区间。

2、拐点和极值点通常是不一样的，两者的定义是不同的。极值点处一阶导数为0，一阶导数描述的是原函数的增减性；拐点处二阶导数为0，二阶导数描述的是原函数的凹凸性。判读方法不同。

3、总结起来，要判断一个函数在某点是否有拐点，我们需要计算函数的二阶导数，并判断其是否为零。如果二阶导数不为零，则函数在该点可能存在拐点，反之则可能没有拐点。

4、方法：（1）求这个函数的二阶导数；（2）若二阶导数在这个点的左边和右边的正负性不同，则这个点就是拐点；若在这个点的左边和右边的正负性相同，则这个点就不是拐点。

The End