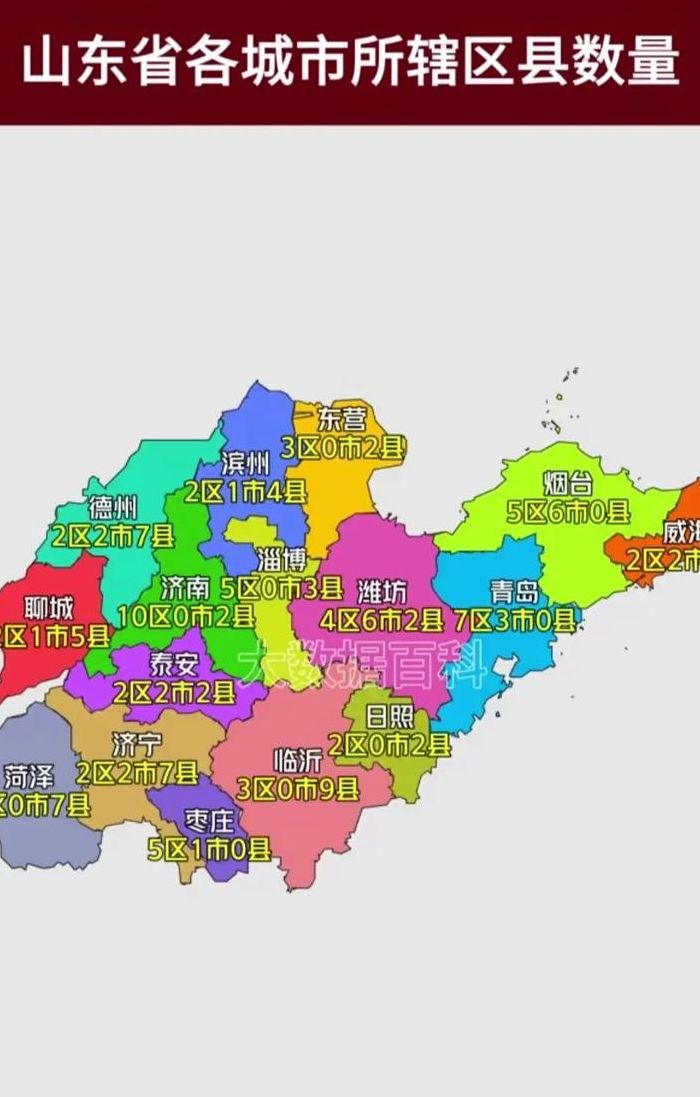
错位排列的问题12345的错位排列分别是多少呢求错位排列的公式是_百度...
1、当n=5时,数字1, 2, 3, 4, 5的错位排列数量可以通过上述公式计算得出,结果为44。这个公式不仅适用于5个元素的错位排列,还可以推广到更多元素的错位排列问题。错位排列的应用广泛,例如在密码学中,可以通过错位排列生成复杂的密码,提高安全性。
2、一个元素的错排为0个。两个元素的错排为1个,三个元素的错排为2个,四个元素的错排为9,五个元素的错排为44。
3、D2=1,D3=2,D4=9,D5=44。
4、错位排列的公式为 P = n! (1 - 1/1! + 1/2! - 1/3!……(-1)^n/n!)使用数学的容斥原理,设S为n个元素全排列集合,S(i)为第i个元素固定的全排列集合。则S-∪{1≤i≤n}Si为错位排列的集合。
5、错位排列的公式为:P = n!^n/n!),其中n表示元素的数量。公式解释:这个公式利用了容斥原理来计算错位排列的个数。容斥原理是一种计算集合并集大小的方法,通过交替加减各个集合的大小以及它们的交集大小来得到最终结果。计算过程:全排列总数:首先计算n个元素的全排列总数,即n!。
6、错位排列的公式为D=n!。解释如下:错位排列问题是指在一个全排列中,每个元素都不在原来的位置上,这种排列的数量即为错位排列数。公式的具体计算方法是基于每个元素的放置方式来计算的。在每一个位置上考虑选择放置哪个元素,这样的选择会有两种可能:要么放在正确的位置,要么放在错误的位置。
错位问题具体是什么?
1、在数学中,错位排列是一个有趣的问题。给定一组元素,如何排列这些元素,使得每个元素都不在原来的位置上?这可以通过公式P=n!(1-1/1!+1/2!-1/3!……(-1)^n/n!)来解决。这个公式基于数学的容斥原理。设S为n个元素全排列的集合,S(i)表示第i个元素固定的全排列集合。
2、错位排列问题就是指一种比较难理解的复杂数学模型,是伯努利和欧拉在错装信封时发现的,因此又称伯努利-欧拉装错信封问题。
3、错位排列问题是一个古老的问题,最先由贝努利(Bernoulli)提出,其通常提法是:n个有序元素,全部改变其位置的排列数是多少?所以称之为“错位”问题。大数学家欧拉(Euler)等都有所研究。下面先给出一道错位排列题目,让考友有直观感觉。
错位排列的公式是什么?
错位排列的问题可以通过以下公式来描述和计算:错位排列的公式为:P = n!^n/n!),其中n表示元素的数量。公式解释:这个公式利用了容斥原理来计算错位排列的个数。容斥原理是一种计算集合并集大小的方法,通过交替加减各个集合的大小以及它们的交集大小来得到最终结果。
在数学中,错位排列是一个有趣的问题。给定一组元素,如何排列这些元素,使得每个元素都不在原来的位置上?这可以通过公式P=n!(1-1/1!+1/2!-1/3!……(-1)^n/n!)来解决。这个公式基于数学的容斥原理。设S为n个元素全排列的集合,S(i)表示第i个元素固定的全排列集合。
错位排列是指在一个排列中,元素之间的相对顺序都不相同。对于一个n个元素的错位排列,其计算公式为:D(n) = n!(1 - 1/1! + 1/2! - 1/3! + ... + (-1)^n/n!)其中,D(n)表示n个元素的错位排列的总数。解释:- n! 表示n的阶乘,表示从n到1的连续自然数的乘积。
错位排列的公式为D=n!。解释如下:错位排列问题是指在一个全排列中,每个元素都不在原来的位置上,这种排列的数量即为错位排列数。公式的具体计算方法是基于每个元素的放置方式来计算的。在每一个位置上考虑选择放置哪个元素,这样的选择会有两种可能:要么放在正确的位置,要么放在错误的位置。
错排公式1到9的计算公式为D(n)=(n-1)*(D(n-1)+D(n-2)。错排问题,是组合数学中的问题之一。考虑一个有n个元素的排列,若一个排列中所有的元素都不在自己原来的位置上,那么这样的排列就称为原排列的一个错排。现代数学集合论中,元素是组成集的每个对象。
09公务员辅导:排列组合问题之错位排列问题
1、错位排列问题是一个古老的问题,最先由贝努利(Bernoulli)提出,其通常提法是:n个有序元素,全部改变其位置的排列数是多少?所以称之为“错位”问题。大数学家欧拉(Euler)等都有所研究。 下面先给出一道错位排列题目,让考友有直观感觉。
2、错位排列问题就是指一种比较难理解的复杂数学模型,是伯努利和欧拉在错装信封时发现的,因此又称伯努利-欧拉装错信封问题。
3、错位重排定义:举个栗子,假设有4个人,每个人有一个书包,现4人从这4个书包中随机背起一个,结果恰好每人背的都不是自己的书包,即为错位重排。(即把每个人都排到了和之前不同的位置上)这是排列组合中的一个非常特殊的题型,一般需要我们记住对应的结论。
4、错位全排列问题,即在装错信封问题中,涉及[公式] 封信与[公式] 个信封的错位排列计数。虽然枚举法在小规模下有效,但随着信封数量增加,计算复杂性剧增。这时,利用排列组合理论和容斥原理可以简化计算。首先,从[公式] 封信的组合总数为[公式] 种方法着手,但需减去重复的装对情况。
5、排列组合问题在行测数量关系中一直是考生们的难点之一,尤其是错位排列问题,它是一个古老而复杂的问题。尽管如此,错位排列问题有其解决之道。关键在于总结规律并牢记公式,这样在考试时就能快速准确地找到解题关键。题干特征描述了N个人和n个物品的对应关系,规定每个人不能使用自己的物品。
5个数错位排列的问题
1、当n=5时,数字1, 2, 3, 4, 5的错位排列数量可以通过上述公式计算得出,结果为44。这个公式不仅适用于5个元素的错位排列,还可以推广到更多元素的错位排列问题。错位排列的应用广泛,例如在密码学中,可以通过错位排列生成复杂的密码,提高安全性。
2、错位排列问题是一个古老的问题,最先由贝努利(Bernoulli)提出,其通常提法是:n个有序元素,全部改变其位置的排列数是多少?所以称之为“错位”问题。大数学家欧拉(Euler)等都有所研究。下面先给出一道错位排列题目,让考友有直观感觉。
3、当小球数为4时,全错位排列的数量为9种。对于5个小球,错位排列的数量增加到了44种。而当小球数增加到6时,全错位排列的数量达到了265种。这组数字0、4265其实遵循着一种特定的规律,值得我们去探索。通过上述例子,我们可以总结出,5个小球的全错位排列共有44种方法。
4、如果有n个对象,则错位重排的情况数用Dn表示,需要大家了解的是:D2=1,D3=2,D4=9,D5=44。
5、种。一个元素的错排为0个。两个元素的错排为1个,三个元素的错排为2个,四个元素的错排为9,五个元素的错排为44。错排问题:n个有序的元素应有n个不同的排列,如若一个排列使得所有的元素不在原来的位置上,则称这个排列为错排;有的叫重排。
文章声明:以上内容(如有图片或视频亦包括在内)除非注明,否则均为网友提供,转载或复制请以超链接形式并注明出处。