托勒密定理（托勒密定理什么时候学）

托勒密定理公式

托勒密定理公式如下：托勒密定理公式是一个用于计算四边形对角线和边长之间关系的几何定理。该定理得名于古希腊数学家托勒密，在他的著作《高等数学》中首次提出并证明了这个定理。在一个四边形ABCD中，假设AB、BC、CD和DA代表四边形的边长，AC和BD代表对角线的长度。

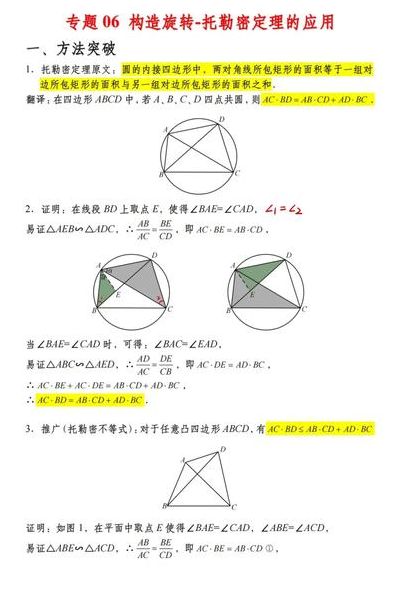
托勒密定理是指：圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。 定理表述：圆的内接四边形中，两对角线所包矩形的面积等于 一组对边所包矩形的面积与另一组对边所包矩形的面积之和。 从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质。

托勒斯定理可以推广出正弦、余弦的和差公式及一系列的三角恒等式。托勒密不等式：凸四边形的两组对边乘积和不小于其对角线的乘积，取等号当且仅当共圆或共线。

将（1）和（2）相加，得到AC（BE+ED）等于AB·CD与AD·BC之和。如果四边形ABCD是圆的内接四边形，当BE+ED等于BD时，等式成立，这就是著名的托勒密定理。在复数表示法中，将顶点A、B、C、D的坐标表示为复数，利用复数恒等式和三角不等式，可以进一步证明托勒密定理是圆内接四边形性质的体现。

托勒密定理是一个关于凸四边形的重要几何性质。根据这个定理，对于任意一个凸四边形ABCD，其对角线AC和BD的乘积与两边AB和CD、AD和BC的乘积之和之间存在不等关系，即AC·BD≤AB·CD+AD·BC。

托勒密定理的证明

以下是托勒密定理的证明：圆内四边形的两组对边乘积之和等于两对角线的乘积。

如果四边形ABCD是圆的内接四边形，当BE+ED等于BD时，等式成立，这就是著名的托勒密定理。在复数表示法中，将顶点A、B、C、D的坐标表示为复数，利用复数恒等式和三角不等式，可以进一步证明托勒密定理是圆内接四边形性质的体现。

托勒密定理证明过程如下：设四边形ABCD的对角线AC和BD互相垂直，O为四边形的内心，r为内接圆的半径。则由内切圆的性质可以得到AO=CO=r和BO=DO=r。通过勾股定理可以得到AB=AO+BO，CD=CO+DO。

托勒密定理是什么

托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。 原文：圆的内接四边形中，两对角线所包矩形的面积等于 一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

总结来说，托勒密定理是一个关于圆内接四边形边角关系的重要定理，它在几何学中占据着基础的地位，对于理解和应用三角函数具有深远影响。

托勒密(Ptolemy)定理指出，圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。在直线上，托勒密定理同样成立，这时也称为欧拉定理。托勒密定理的逆定理同样成立：一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆。琴生不等式是丹麦数学家琴生于1905年到1906年间建立的。

平面几何中有许多著名的定理，以这些定理为基础，可以推出不少精彩的结论。托勒密定理就是中学数学中熟知的定理之一，它是一个关于四边形的定理：圆内接四边形中两组对边的积的和等于两对角线的积。”托勒密（约90-168）是古希腊亚历山大后期重要的数学家、天文学家和地理学家。

等腰梯形(英文：isosceles trapezium)按照数学领域可定义为：一组对边平行(不相等)，另一组对边不平行但相等的四边形。等腰梯形是一种特殊的梯形。性质 等腰梯形同一底上的两个内角相等。两腰相等，两底平行，对角线相等 。由托勒密定理可得等腰梯形ABCD，有AB*CD+BC*AD=AC*BD。

托勒密定理运用要点

1、在几何学中，托勒密定理揭示了一个关键的关系，即当四个点A、B、C、D满足特定条件时，等式(a-b)(c-d)与(a-d)(b-c)的辐角相等。这个条件实际上等价于这四个点共处于同一个圆周上，不论它们在空间中的位置如何，只要共享一个圆，该定理就成立。

2、托勒密定理的运用要点：等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。四点不限于同一平面。欧拉定理：在一条线段上AD上，顺次标有B、C两点，则AD·BC+AB·CD=AC·BD。

3、托勒密定理在几何学中有着广泛的应用，例如，它可用于证明帕斯卡定理和布利安萨定理等重要的几何定理。 在代数领域，托勒密定理同样重要，它有助于解决线性代数中的问题，如矩阵的逆和行列式的计算。 四边形的不稳定性是其一个显著特点。

4、应用：计算矩形的对角线：对于一个矩形，它的边长分别为a和b，根据托勒密定理，矩形的对角线长度可以通过以下公式计算：AC=√(a^2+b^2)。验证正方形：对于一个四边形，如果它的边长相等且对角线长度相等，那么根据托勒密定理，可以得出以下结论：AB=BC=CD=DA，AC=BD。

托勒密定理推论

托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。 原文：圆的内接四边形中，两对角线所包矩形的面积等于 一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

推论：任意凸四边形ABCD，必有AC·BD≤AB·CD+AD·BC，当且仅当ABCD四点共圆时取等号。托勒密定理的逆定理同样成立：一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆。

托勒密定理是一个关于凸四边形的重要几何性质。根据这个定理，对于任意一个凸四边形ABCD，其对角线AC和BD的乘积与两边AB和CD、AD和BC的乘积之和之间存在不等关系，即AC·BD≤AB·CD+AD·BC。

托勒密定理：圆内接四边形两条对角线的乘积等于两对对边乘积之和。如下图所示，ABCD为圆内接四边形，则对角线AC与BD的乘积等于一对对边AB与CD的乘积加上另一对对边AD与BC的乘积，即AC·BD=AB·CD+AD·BC。证明：（1）如下图所示。

托勒密定理的推广

1、托勒斯定理可以推广出正弦、余弦的和差公式及一系列的三角恒等式。托勒密不等式：凸四边形的两组对边乘积和不小于其对角线的乘积，取等号当且仅当共圆或共线。

2、托勒密定理在其基础上得到了进一步的推广。原定理指出，对于凸四边形，其任意两组对边的乘积之和不小于其对角线的乘积，当且仅当四边形共圆或共线时，这个不等式才会取等号。这个定理可以通过复数的性质进行直观理解。

3、托勒密定理的推广：四边形两对边乘积之和大于等于其对角线乘积 取等号时，该四边形是圆内接四边形。

4、托勒密定理不教的原因可能与其涉及的数学知识点有关。托勒密定理是圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积，这一定理同样可以推广为圆的内接凸n边形两对对边乘积的和等于n边形的对角线乘积。

5、方法一：（以下是推论的证明，托勒密定理可视作特殊情况。

6、托勒密(Ptolemy)定理指出，圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。在直线上，托勒密定理同样成立，这时也称为欧拉定理。托勒密定理的逆定理同样成立：一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆。

The End