什么叫方阵（什么叫方阵的特征值）

线性代数什么叫方阵

1、方阵是指行数和列数相等的矩阵，也就是一个n×n的矩阵。方阵具有特殊的性质和重要的应用。它们可以表示线性变换、解线性方程组、计算特征值和特征向量等。方阵的对角线上的元素称为主对角线元素，其他元素称为非主对角线元素。方阵在许多领域中都有广泛的应用，如物理学、工程学、计算机科学等。

2、方阵就是行数与列数一样多的矩阵。在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。

3、方阵是一种常见的几何形态，指行数和列数相等的矩阵，方阵的三个重要性质有对角线性质、转置性质、行列式性质。对角线性质 方阵的对角线元素之和等于主对角线元素的平方和。这一性质在矩阵运算和线性变换中有重要应用，当需要对矩阵进行某些操作时，了解对角线元素的关系可以帮助简化计算过程。

4、行列式的定义：行列式是线性代数中一种重要的数学概念，它是一个方阵的固有属性。在高等数学中，行列式通常用于描述线性变换在空间中的表现形式。行列式的定义是：由n×n个数排列成一个n阶方阵，这些数的乘积M，即为该方阵的行列式。行列式可以看作是一种计算方阵的方法，它具有一些重要的性质。

数学中的方阵什么意思

1、数学中的方阵的意思：矩阵。数学中的方阵就是矩阵的意思，在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。

2、数学中的方阵是一种特殊的矩阵排列。其主要特点是每行和每列的元素数量相等，排列整齐。方阵是数学中的一个重要概念，尤其是在线性代数中。以下是对方阵的 方阵的基本定义 方阵是一种特殊的矩阵。所谓的矩阵，是由若干行和若干列组成的一个数字阵列。

3、数学方阵，是指行与列构成的矩阵，其元素通常是实数或复数。在数学领域，方阵是矩阵的一种特殊形式，它的行和列数目相等。方阵是矩阵理论中研究的重点对象之一，是线性代数和数学分析的基本工具之一。数学方阵在科学研究、技术应用、金融投资等领域都有广泛应用。

矩阵.方阵以及行列式的区别

1、矩阵是有若干行，若干列，组成的元素阵列 本质上是一组有严格位置定义的元素排列。而方阵，是特殊的矩阵，即满足行列数相等的矩阵。行列式，是方阵的一个属性，本质上是一个数值，根据一定算法可以求出一个方阵的行列式。

2、方阵是矩阵的一种特殊类型，而行列式，是方阵对应的一个数值，即行列式本质上是数，不是矩阵。

3、总的来说，矩阵和方阵是数学中的两个基本概念，而行列式则是方阵特有的一个特性，它为我们理解和处理矩阵问题提供了关键的数值信息。

什么叫方阵

1、方阵是指排列为正方形或矩形的一种阵列形式。方阵是一种特殊的阵列形式，通常用于军事、艺术展示或计算场合。以下是关于方阵的详细解释： 方阵的基本定义：方阵是一种排列形式，其中的元素按照一定的行和列进行整齐排列，形成一个矩形或正方形的形状。这种阵列可以是人员、武器、物品等组成的。

2、意思很多 选自百科 亦作方陈。方形之军阵。古代阵法有方、圆、雁行、钩行等多种。见《孙膑兵法．十阵》。指麻将牌局。四人对局、开局前、每人理十七或十八墩构成方形故称。数学中，指行数及列数皆相同的矩阵，即方块矩阵。战术中，可以指希腊方阵、罗马方阵（鱼鳞阵）。

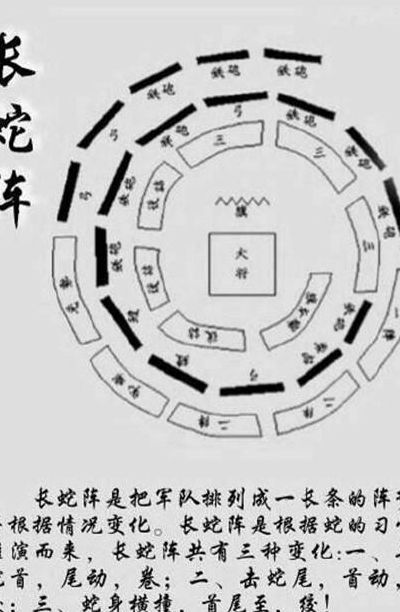
3、方阵是古代军队作战时采用的一种队形，是把军队在野外开阔地上排列成方形阵式。远古方阵由前军、中军和后军相互嵌套排列而成，方阵平面呈现“回”字形状，反映出远古观念中的一种政治地理结构，来源于“天圆地方”的宇宙观。

4、方阵其实就是特殊的矩阵，当矩阵的行数与列数相等的时候，我们可以称它为方阵，比如说：某一矩阵的行数与列数都是5，我们可以叫它为5阶方阵。矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。

5、方阵是古代军队在战斗中使用的一种队形，即在野外将军队排成方阵。古代方阵由前军、中军、后军组成。方阵平面呈回形，反映了古代观念中的一种政治地理结构，源于天地的宇宙观。 在数学中，n阶矩阵称为n阶方阵，即方阵是行数和列数相同的矩阵。

6、方阵是指行数和列数相等的矩阵，也就是一个n×n的矩阵。方阵具有特殊的性质和重要的应用。它们可以表示线性变换、解线性方程组、计算特征值和特征向量等。方阵的对角线上的元素称为主对角线元素，其他元素称为非主对角线元素。方阵在许多领域中都有广泛的应用，如物理学、工程学、计算机科学等。

The End