黎曼空间（黎曼空间坐标系）

黎曼空间与欧几里德空间区别

1、性质不同黎曼空间是一种矢量空间，它满足空间中存在度规张量；欧氏空间是一个特别的度量空间，在包含了欧氏几何和非欧几何的流形的定义上发挥了作用。三角形内角和不同黎曼空间中，三角形的内角和大于180度，圆周率小于π；欧几里德空间中，三角形的内角和等于180度，圆周率等于π。

2、综上所述，黎曼空间和欧几里德空间的主要区别在于它们的几何形态和性质。黎曼空间允许弯曲和扭曲的几何结构，适用于描述复杂的自然现象；而欧几里德空间则是平直的空间模型，广泛应用于日常生活和工程领域。两者各有其独特的优势和适用范围，共同构成了几何学的重要组成部分。

3、当一个线性空间定义了内积运算之后它就成为了欧几里德空间。02：黎曼空间常曲率黎曼空间 Riemannian space of constant curvature 截面曲率为常数的黎曼流形，它包括了欧氏空间、球面、双曲空间为其特例。在曲面论中，高斯曲率K为常数的曲面局部地为球面(K0)，平面（K=0）或双曲平面(K0)。

4、欧氏空间和黎曼空间是数学中两种重要的几何结构。欧几里德空间，也称平直空间，是二维和三维空间的扩展，适用于任意维度的坐标系统，是有限维实内积空间的典型例子。它不仅在度量空间和拓扑性质研究中占据核心地位，而且在微分几何中，尤其是对定义流形的几何概念和微分性质的理解中发挥着关键作用。

5、欧几里德几何有时就指平面上的几何，即平面几何。三维空间的欧几里德几何通常叫做立体几何。高维的情形请参看欧几里德空间。数学上，欧几里德几何是平面和三维空间中常见的几何，基于点线面假设。数学家也用这一术语表示具有相似性质的高维几何。黎曼流形上的几何学。

非线性空间存在吗

存在。非线性空间即黎曼空间，是一个多维空间，比如平行空间、十度空间、量子空间等等。过去、现在和未来，都只是某个无限大的黎曼空间网格上不同的点而已，没有先后之别。在这个多维空间里，所有时间段里发生的事情，都可以成为单独呈现的空间。

所以总体上来说，非线性无处不在，线性是偶发，而且也是平均或统计意思上的。正因为如此，非线性世界的情况多变且复杂，这个找规律和预测提供了障碍。比如天气预报，一般只能预报三天的天气，因为天气的形成，有赖于局部的空气中各种小物质的大量相互作用，参数和属性极多，几乎无法预测。

简单来说，如果一个空间中的所有向量都满足乘一个常数后或者和其它向量相加后仍然在这个空间里，那么这个空间就是线性空间。

因为使用了较少的颜色（相对于线性颜色空间），因此会得到比较好的渲染效率以及较低的渲染能力需求。但是图像会存在失真（偏暗，因为亮部细节表现不够）等一系列问题。线性空间-Linear 是数值强度值，与感知强度是成正比例对应的。

非线性关系应该叫空间关系，两点确定一条直线，线性关系在这线上，非线性关系应该是既定的直线外的点存在。一般认为时间是线性的，因为时光不能倒流，一直往前走。生物学，研究生命的起源之类的属于线性和时间关系。

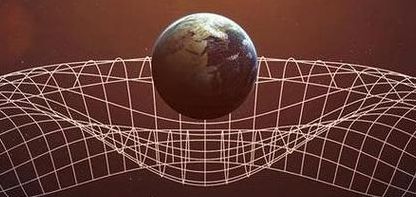
也正是爱因斯坦狭义相对论和广义相对论证明了的。时间流逝的快慢跟运动速度有关，空间的平滑程度也跟速度有关，加速度即引力效应也是空间扭曲的本质原因。这些都是通过实验观测证实了的理论。所以说我们的宇宙是非线性的。强有力的一个证据就是黑洞里的空间和事件曲率都是无穷大的，极度扭曲的。

闵氏空间和黎曼空间的区别有哪些?

1、首先，闵氏空间和黎曼空间的定义不同。闵氏空间是一个具有欧几里得度量的n维实向量空间，而黎曼空间则是一个具有黎曼度量的n维实向量空间。欧几里得度量和黎曼度量是两种不同的度量方式，它们对空间中的点之间的距离进行定义的方式不同。其次，闵氏空间和黎曼空间的性质也有所不同。

2、理论物理：闵氏时空是爱因斯坦广义相对论的基础，它描述了引力场中的物体运动规律。黎曼空间则是研究量子力学的数学工具，如路径积分等方法都需要用到黎曼空间。天体物理：闵氏时空和黎曼空间在宇宙学、黑洞理论、宇宙膨胀等方面有重要应用。

3、从切丛的旋律中，我们可以谱写出半黎曼度规的交响曲。这是一种线性映射，将切丛与实数R紧密联系，其行列式犹如旋律的节奏，非零的它定义了黎曼空间的内敛热情。若它拥抱正定性，便奏响了黎曼流形的和谐篇章；而伪黎曼空间，如闵氏空间，它的距离旋律则略显深沉。

4、接下来说说空间吧！普通人（包括牛顿）会认为，空间就是空间啊，看不见摸不着，但是空间却装着我们，空间本身是平直均匀的。但是爱因斯坦说，空间均匀个毛线啊！空间和时间都是对物质运动的不同形式上的度量。空间自然受到物质的影响，空间中存在一点，这点周围就不均匀了，也不平直的。

解释一下:欧氏空间和黎曼空间

1、：欧几里德空间(Euclidean Space)，简称为欧氏空间(也可以称为：平直空间)，在数学中是对欧几里德所研究的2维和3维空间的一般化。这个一般化把欧几里德对于距离、以及相关的概念长度和角度，转换成任意数维的坐标系。这是有限维、实和内积空间的“标准”例子。

2、欧氏空间和黎曼空间欧氏空间是一种特殊的向量空间，也称为欧几里得空间。它是一个具有有限维度的实数向量空间，其中的向量可以表示点或方向，并且具有特定的距离度量方式，即欧几里得距离。在这种空间中，几何形态与在现实世界中的直观感受相似，线段最短且垂直于两点连线的直线通过这两点的中点。

3、欧氏空间和黎曼空间是数学中两种重要的几何结构。欧几里德空间，也称平直空间，是二维和三维空间的扩展，适用于任意维度的坐标系统，是有限维实内积空间的典型例子。它不仅在度量空间和拓扑性质研究中占据核心地位，而且在微分几何中，尤其是对定义流形的几何概念和微分性质的理解中发挥着关键作用。

4、欧氏空间和黎曼空间欧氏空间是一种特殊的向量空间，也称为欧几里得空间。它是一个具有有限维度的实数向量空间，其中两点之间的距离可以通过欧几里得距离公式计算得出。这个距离计算公式就是我们常说的两点间的直线距离，在数学和物理学中有广泛的应用。

黎曼空间是什么

1、常曲率黎曼空间 Riemannian space of constant curvature 截面曲率为常数的黎曼流形，它包括了欧氏空间、球面、双曲空间为其特例。在曲面论中，高斯曲率K为常数的曲面局部地为球面(K0)，平面（K=0）或双曲平面(K0)。在高维时高斯曲率的自然推广为截面曲率(见黎曼几何学)。

2、黎曼空间是一种更广义的几何空间概念，它允许在非平坦的几何结构中研究几何对象的性质和变换。黎曼空间允许存在弯曲和扭曲的几何形态，这使得它可以描述更加复杂的自然现象，例如引力场的弯曲时空等。黎曼几何通常涉及到曲面或流形的微分结构，并通过对距离、角度和曲率的测量来研究几何对象的属性和相互关系。

4、黎曼空间是一种矢量空间，它满足空间中存在度规张量；欧氏空间是一个特别的度量空间，在包含了欧氏几何和非欧几何的流形的定义上发挥了作用。三角形内角和不同黎曼空间中，三角形的内角和大于180度，圆周率小于π；欧几里德空间中，三角形的内角和等于180度，圆周率等于π。

The End