中点四边形（中点四边形的周长）

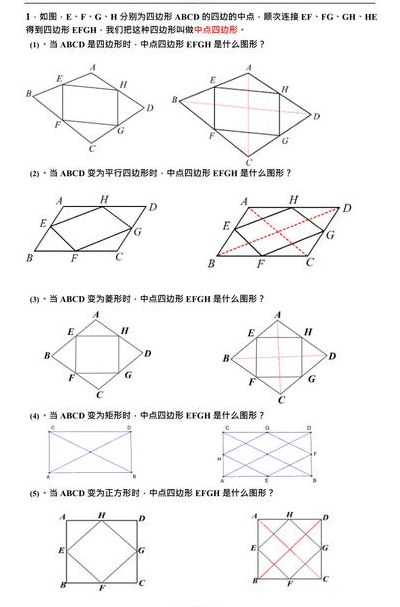
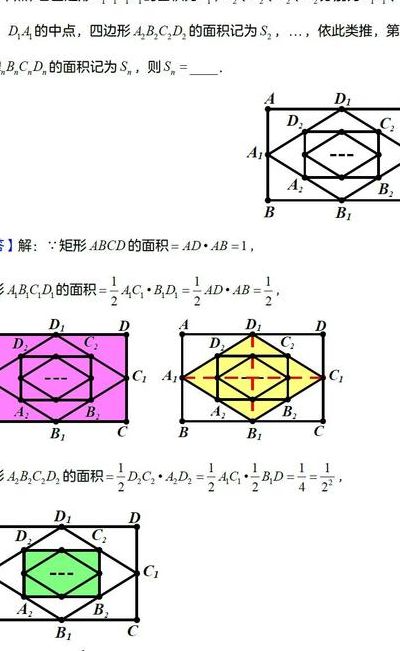
中点四边形是什么?

1、任意四边形中点连线形成四边形是平行四边形。相邻两条边中点连线平行于一条对角线，另外两条边中点连线平行于同一条对角线。所以这两条中点连线互相平行。同理，另外两条中点连线也互相平行。所以，这些中点连线形成的四边形一定是平行四边形。

2、中点四边形的定义 在一个多边形中，通过连接各边的中点所组成的四边形，被称为中点四边形。详细解释如下：定义介绍 在多边形的几何学中，当我们选择多边形每条边的中点，并将这些中点依次连接时，所形成的封闭图形即为中点四边形。

3、依次连接任意四边形各边中点所得的四边形称为中点四边形。在同一个二维平面内，由两组平行线段组成的闭合图形，称为平行四边形。如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等。平行四边形定义 两组对边分别平行的四边形叫做平行四边形。平行四边形属于平面图形。

4、这个概念指的是，从一个四边形的每一边中点出发，将它们连接起来所构成的新四边形。简单来说，就是将原四边形的中心点连成的新图形。一个显著的特性是，中点四边形必定是一个平行四边形。

5、中点四边形是指在一个四边形中，其所有边的中点连接而成的四边形。详细解释如下：在一个四边形中，如果我们连接其各边的中点，构成的新四边形就称为中点四边形。具体来说，这个新四边形的顶点分别是原四边形各边的中点。

中点四边形的定义?

1、中点四边形的定义 在一个多边形中，通过连接各边的中点所组成的四边形，被称为中点四边形。详细解释如下：定义介绍 在多边形的几何学中，当我们选择多边形每条边的中点，并将这些中点依次连接时，所形成的封闭图形即为中点四边形。

2、定义：依次连接任意四边形各边中点所得的四边形称为中点四边形。不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形。中点四边形的面积为原四边形面积的一半。

3、中点四边形，顾名思义，是指通过连接一个四边形各边的中点而形成的新四边形。这个定义适用于任何形状的四边形，无论是规则的还是不规则的。其核心特性在于，无论原四边形如何变化，其中点四边形始终保持平行四边形的特性。这是由于中点四边形的对边是原四边形对边中点的连线，平行性得以保持。

4、任意四边形中点连线连成的四边形总是平行四边形，菱形中点连线所得的图形是矩形，正方形中点连线所得的图形是正方形，矩形中点连线所得的图形是菱形，等腰梯形中点连线所得的图形是菱形。这个定义同样适用于凹四边形和折四边形。

什么是中点四边形

依次连接任意四边形各边中点所得的四边形称为中点四边形。在同一个二维平面内，由两组平行线段组成的闭合图形，称为平行四边形。如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等。平行四边形定义 两组对边分别平行的四边形叫做平行四边形。平行四边形属于平面图形。

中点四边形是指在一个四边形中，其所有边的中点连接而成的四边形。详细解释如下：在一个四边形中，如果我们连接其各边的中点，构成的新四边形就称为中点四边形。具体来说，这个新四边形的顶点分别是原四边形各边的中点。

简单来说，就是将原四边形的中心点连成的新图形。一个显著的特性是，中点四边形必定是一个平行四边形。这个结论可以通过一个直观的证明来理解：首先，连接原四边形的对角线，然后观察这两个对角线在中点四边形中所形成的两个三角形。

中点四边形 定义：依次连接任意四边形各边中点所得的四边形称为中点四边形。不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形。中点四边形的面积为原四边形面积的一半。

中点四边形是由任意四边形各边中点所构成的四边形。在二维平面上，由平行线段组成的闭合图形称为平行四边形。四边形若为平行四边形，则其对边相等。菱形的中点四边形会形成矩形，矩形的中点四边形则会变为菱形，而等腰梯形的中点四边形则为菱形，正方形的中点四边形依旧是正方形。

中点四边形，是一种由任意四边形各边中点依次连接而成的四边形。不论原始四边形形状如何变化，形成的中点四边形总是平行四边形。此四边形面积恰好是原始四边形面积的一半。证明如下：设原始四边形为ABCD，其各边中点分别为E、F、G、H，连接EFGH，即为中点四边形。连接对角线BD。

The End