切割线定理证明（切割线定理证明3种方法带图）

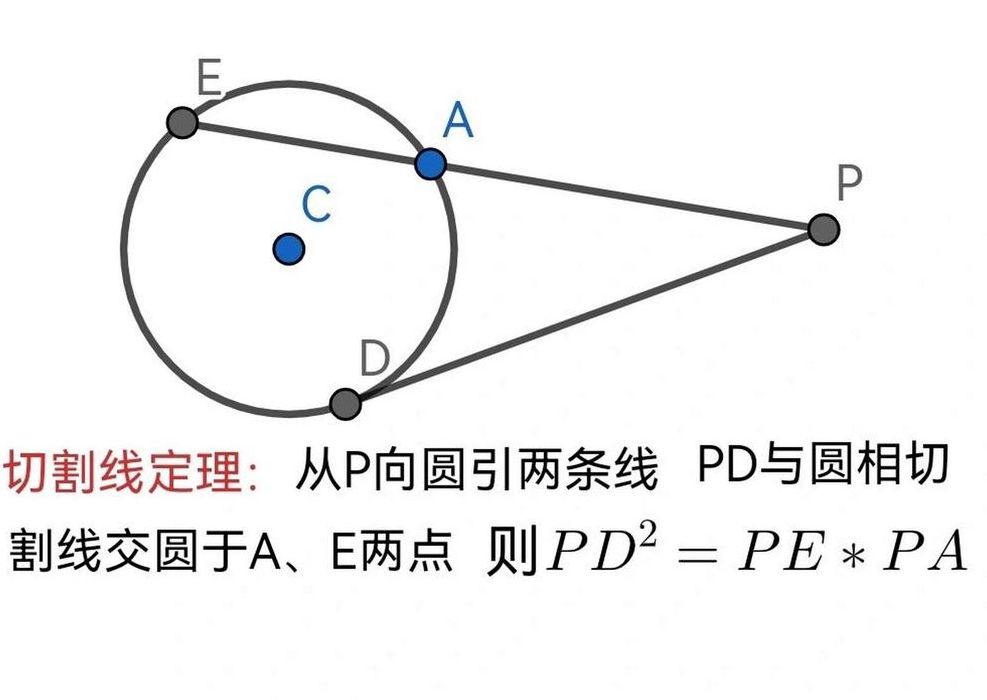
切割线定理的证明

1、切割线定理的证明如下：切割线定理：从圆外一点引圆的切线和割线，切线长是割线与圆直径的商的2倍。证明：设圆外一点为P，圆心为O，割线与圆的交点为A、B，切点为C，则有：根据切割线定理，有：PA·PB=PC·PO。因为PO是直径，所以：PO=2r。所以：PA·PB=（PC·PO）/（PO/2）。

2、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。切割线定理的推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。切割线定理的证明 设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT=PA·PB。

3、切割线定理证明过程如下：直线ABP和CDP是自点P引的两条割线，则PA·PB=PC·PD证明：连接AD、BC。∠A和∠C都对弧BD由圆周角定理，得∠A=∠C，又∠APD=∠CPB△ADP∽△CBPAP：CP=DP：BP也就是AP·BP=CP·DP比较割线定理与相交弦定理，切割线定理统称为圆幂定理。

4、证明：∵PA是圆O的切线 ∴∠PAE=∠AFP(弦切角定理)而∠APE=∠FPA ∴△APE∽△FPA ∴AP/FP=PE/PA ∴PA=PE*PF 于是切割线定理得证 祝学习进步，望采纳。不懂得欢迎追问。。

切割线定理证明

1、切割线定理证明：设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT^2=PA·PB。证明过程如下：连接AT，根据弦切角定理，∠PTB=∠PAT。同时，∠P=∠P为公共角。根据两角对应相等，两三角形相似的原理，得出△PBT∽△PTA。由此得到比值关系：PB：PT=PT：AP，即PT^2=PB·PA。

2、切割线定理公式及证明如下：切割线定理是指从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。证明过程：设ABP是圆O的一条割线，PT是圆O的一条切线，切点为T。

3、切割线定理的证明如下：切割线定理：从圆外一点引圆的切线和割线，切线长是割线与圆直径的商的2倍。证明：设圆外一点为P，圆心为O，割线与圆的交点为A、B，切点为C，则有：根据切割线定理，有：PA·PB=PC·PO。因为PO是直径，所以：PO=2r。所以：PA·PB=（PC·PO）/（PO/2）。

4、切割线定理公式是PT=PA·PB。证明上：设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT=PA·PB，连接AT， BT。∵∠PTB=∠PAT（弦切角渣前定理）。切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

怎么证明切割线定理、割线定理、弦切角定理?

1、切割线定理证明过程如下：以点O为圆心，TC为割线，TC与圆O相切于点C。连接AC、BC，观察到弦切角∠TCB对弧BC，而圆周角∠A同样对弧BC。根据弦切角定理，可以得出∠TCB等于∠A。进一步，我们可以发现∠ATC与∠BTC相等。因此，△ACT与△CBT在角度上完全对应，可以判断出这两个三角形相似。

2、圆的切割线定理证明如下：切线的判定和性质：切线的判定定理，经过半径的外端并且垂直于这条半径的直线是圆的切线。几何语言：∵l⊥OA，点A在⊙O上，∴直线l是⊙O的切线（切线判定定理）。切线的性质定理：圆的切线垂直于经过切点半径。

3、切割线定理证明 设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT2=PA·PB。证明：连接AT， BT。∵ ∠PTB=∠PAT(弦切角定理)；∠APT=∠TPB(公共角)；∴ △PBT∽△PTA(两角对应相等，两三角形相似)；∴PB：PT=PT：AP；即：PT2=PB·PA。

4、切割线定理从圆外一点引圆的切线和割线，切线长是庆梁枣这点到割线与圆交点的两条线段长的比例中项.是圆幂定理的一种。

5、当我们探讨圆的性质时，一个重要的定理——切割线定理，其陈述是这样的：设在圆⊙O中，ABP是一条割线，PT是一条切线，切点为T，那么PT的平方等于PA和PB的乘积，即PT=PA·PB。下面将给出这个定理的证明过程。首先，连接点A和T，以及点B和T，我们有∠PTB和∠PAT。

6、切割线定理公式及证明如下：切割线定理是指从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。证明过程：设ABP是圆O的一条割线，PT是圆O的一条切线，切点为T。

什么是圆的切割线定理??

圆的切割线定理是指一个切割线与一个圆相交时，切点和切线之间的关系。根据定理，切点和切线之间的长度乘积是一个常数。定理表述：对于一个切割一个圆的切线，设切点为A，切线上的一点为B，圆心为O。

过圆上一点的切线与通过该切点的半径形成直角，这是切线定理的基本规则。这个定理揭示了圆的切线和半径之间的几何关系，为解决圆的切线问题提供了理论基础。圆外某一点到圆的两条切线长度相等，这是圆外一点与圆切线定理的一部分。

切割线定理：从圆外一点引圆的切线和割线，切线长是割线和这点到割线与圆交点的两条线段长的比例中项。与圆相交的直线是圆的割线。切割线定理揭示了从圆外一点引圆的切线和割线时，切线与割线之间的关系。这是一个重要的定理，在解题中经常用到。

切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。是圆幂定理的一种。

切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。切割线定理的推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。切割线定理的证明 设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT=PA·PB。

圆的切割线定理证明如下：切线的判定和性质：切线的判定定理，经过半径的外端并且垂直于这条半径的直线是圆的切线。几何语言：∵l⊥OA，点A在⊙O上，∴直线l是⊙O的切线（切线判定定理）。切线的性质定理：圆的切线垂直于经过切点半径。

The End