二次函数顶点式公式（二次函数顶点式公式推导过程）

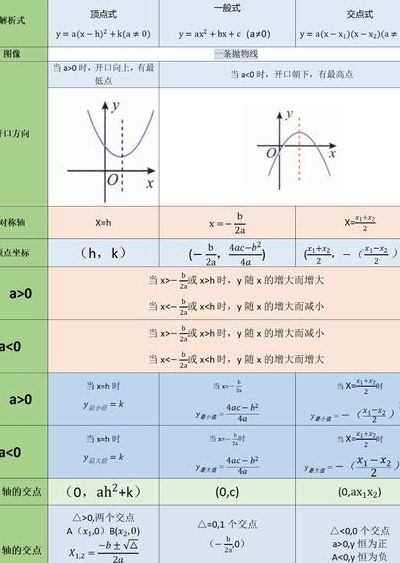
二次函数的顶点公式是什么

二次函数顶点公式：y=a(x-h)+k（a≠0）。顶点P坐标为(h，k)，当h=0时，P在y轴上；当k=0时，P在x轴上，因此h=-b/2a，k=4ac-b/4a。二次函数顶点式的对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax的图像相同。

对于二次函数y=ax^2+bx+c，其顶点为 (-b/2a，(4ac-b^2)/4a)。

二次函数的一般形式：y = ax^2 + bx + c，其中a、b、c为常数，且a ≠ 0。 二次函数的顶点坐标公式：顶点坐标为 (-b/2a， f(-b/2a))，其中f(x) = ax^2 + bx + c。 二次函数的对称轴公式：对称轴方程为 x = -b/2a。

二次函数顶点坐标的公式：(-b/2a，(4ac-b^2)/4a)，二次函数的基本表示形式为y=ax2+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。二次函数表达式为y=ax2+bx+c（且a≠0），其定义是一个二次多项式或单项式。

二次函数的顶点坐标公式

1、对于二次函数y=ax^2+bx+c，其顶点为 (-b/2a，(4ac-b^2)/4a)。

2、顶点坐标公式二次函数Y=a (x-h)2+k二次函数顶点式二次函数顶点公式：y=a(x-h)2+k(a≠0，a、h、k为常数)，顶点坐标为（h，k)，对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax2的图像相同，当x=h时，y最大（小）值=k。

3、二次函数顶点坐标的公式：(-b/2a，(4ac-b^2)/4a)，二次函数的基本表示形式为y=ax2+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。二次函数表达式为y=ax2+bx+c（且a≠0），其定义是一个二次多项式或单项式。

求二次函数顶点坐标的公式!

1、二次函数的顶点坐标公式为 ，其中 h = -b/2a，k = f。这里a、b是二次函数系数，同时需要判断判别式Δ的值来确定函数是否开口向上或向下。在公式使用中需注意二次函数的开口方向和顶点是否存在。对具体题目求解题型需要进行有针对性的灵活运用公式进行计算分析。

2、对于二次函数的标准形式 f = ax + bx + c，其顶点坐标可以通过公式计算得出。这里的顶点指的是函数图像的最高点或最低点。对于开口向上的抛物线，顶点是最低点；对于开口向下的抛物线，顶点是最高点。顶点横坐标的计算：公式中的“-b/2a”表示的是顶点横坐标。

3、二次函数的顶点坐标可以通过配方或者直接代公式求得。配方：将二次函数写成y=a《xh》2+ky=a《xh》^2+ky=a《xh》2+k的形式，其中hhh和kkk就是顶点坐标。

4、当然，如果你觉得记忆公式更为方便，也可以直接记住顶点坐标的计算公式：x=-b/(2a)。通过这个公式，我们可以迅速计算出顶点的x坐标。而顶点的y坐标则由y=(4ac-b^2)/(4a)给出。这个公式简洁明了，适用于所有二次函数。

二次函数顶点坐标公式怎么推导?

1、二次函数顶点坐标公式为（-b/2a，（4ac-b^2）/4a）。完全平方形式推导：考虑一般的二次函数$f(x)=ax^2+bx+c$，其中a≠0。首先，我们可以通过将x的平方项与线性项的系数的一半平方完成平方，即$(x+\frac{b}{2a})^2$。

2、二次函数顶点坐标公式推导过程如下：用来表示二次函数抛物线顶点位置的坐标被叫做二次函数顶点坐标，顶点公式为y=a（x—h）+k（a≠0，k为常数）顶点坐标是【—b/2a，（4ac—b）/4a】。二次函数的一般式为ax+bx+c=z（a≠0）。

3、二次函数顶点坐标公式为：。推导过程如下：二次函数的通用表达式及其特点 二次函数的标准形式为：y = ax + bx + c 。这是一个开口方向的抛物线方程，其中a决定了开口方向及开口大小，b和c是系数，影响抛物线的位置。顶点坐标公式基于这个标准形式推导而来。

4、二次函数顶点坐标的公式是：( -b/2a， (4ac - b^2)/4a )。顶点坐标公式的推导 二次函数的一般形式是y=ax^2+bx+c。为了找到顶点坐标，需要对其进行配方。通过配方，可以得到y=a(x+b/2a)^2+(4ac - b^2)/4a。可以看到x=-b/2a，y=(4ac - b^2)/4a就是二次函数的顶点坐标。

5、二次函数顶点坐标公式的推导过程主要是通过配方法实现的。首先，我们有一个形式为y=ax^2+bx+c的二次函数。为了找到顶点的坐标，我们尝试将其转换为顶点式。具体来说，我们首先将二次项和一次项合并，得到y=a(x^2+bx/a+c/a)。

6、顶点式推导：我们知道二次函数一般表示为y = ax + bx + c的形式。为了得到其顶点坐标公式，我们可以通过配方的方法将其转化为顶点式。配方的过程中，我们会将函数转化为完全平方的形式，从而轻松地找到函数的顶点坐标。

The End