可导一定连续吗（某一点可导一定连续吗）

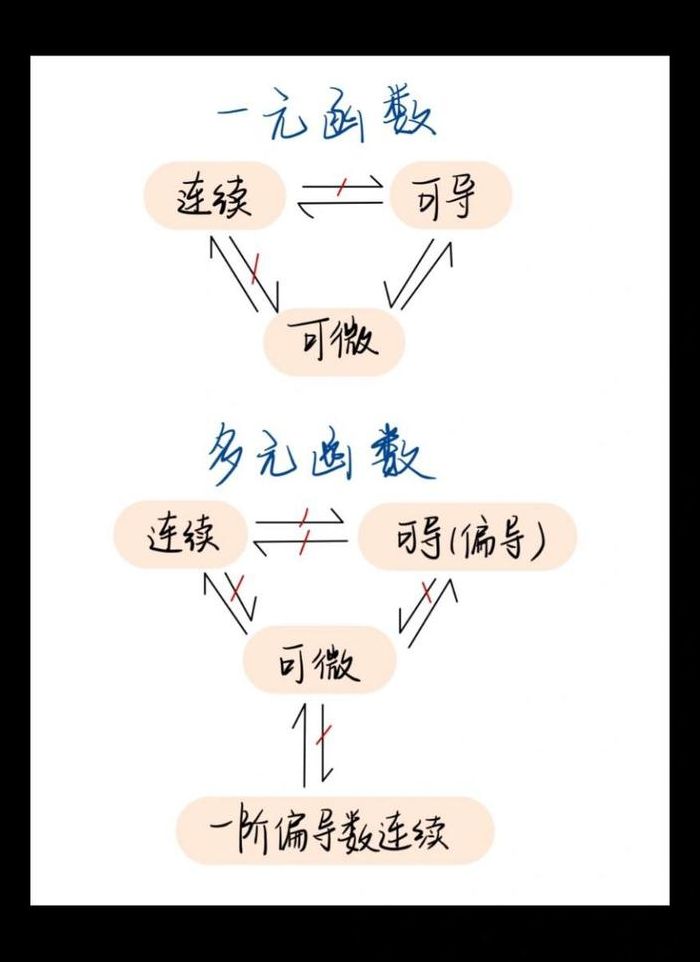
可导必定连续吗?

当然是对的，我们可以证明其逆否命题“可导的函数一定连续”，那么原命题和逆否命题的真伪性一致。就证明了“不连续的函数一定不可导”首先明确一个概念，极限为无穷大，属于极限不存在的情况之一，不是极限存在的情况，极限存在，必须是极限为有限常数。

可导的函数一定连续；不连续的函数一定不可导。可导，即设y=f(x)是一个单变量函数， 如果y在x=x0处存在导数y′=f′(x)，则称y在x=x[0]处可导。如果一个函数在x0处可导，那么它一定在x0处是连续函数。

可导一定连续，连续不一定可导。连续是可导的必要条件，但不是充分条件，由可导可推出连续，由连续不可以推出可导。可以说：因为可导，所以连续。不能说：因为连续，所以可导。可导必连续证明如下图 连续不一定可导。函数可导，导函数不一定连续。

函数可导必须连续吗?

1、当然是对的，我们可以证明其逆否命题“可导的函数一定连续”，那么原命题和逆否命题的真伪性一致。就证明了“不连续的函数一定不可导”首先明确一个概念，极限为无穷大，属于极限不存在的情况之一，不是极限存在的情况，极限存在，必须是极限为有限常数。

2、可导一定连续，连续不一定可导。可以导的函数的话，如果确定-点那么就知道之后一点的走向，不会有突变。可以导的函数的话，如果确定一点那么就知道之后一点的走向，不会有突变。连续的函数不一定可导；可导的函数是连续的函数；越是高阶可导函数曲线越是光滑；存在处处连续但处处不可导的函数。

3、连续函数：函数f(x)在其定义域内的每一点都连续，则称函数f(x)为连续函数。连续性与可导性关系：连续是可导的必要条件，即函数可导必然连续；不连续必然不可导；连续不一定可导。典型例子：含尖点的连续函数。函数可导的充要条件：函数在该点连续且左导数、右导数都存在并相等。

4、可导一定连续，连续不一定可导。连续是可导的必要条件，但不是充分条件，由可导可推出连续，由连续不可以推出可导。可以说：因为可导，所以连续。不能说：因为连续，所以可导。可导必连续证明如下图 连续不一定可导。函数可导，导函数不一定连续。

连续可导的函数一定连续吗?

可导不一定可微 可微不一定连续 所以可导不一定连续 直接举例：有f(x，y) 函数：当 x=0， y=0 时： f(x，y) = 0 其他情况时： f(x，y) = (xy)/(x^2 + y^2)这个函数就是可导，但是不连续。在(0，0)位置不连续。

对一元函数来说：一函数存在导函数，说明该函数处处可导，故原函数一定连续。（可导一定连续）如果一个函数在x0处可导，那么它一定在x0处是连续函数。函数可导定义：（1）设f(x)在x0及其附近有定义，则当a趋向于0时，若 [f(x0+a)-f(x0)]/a的极限存在， 则称f(x)在x0处可导。

“连续可导”在不同的时候可能有不同指代，但是大多数时候还是说函数本身连续，并且进一步的，函数可导。此时函数的导函数不一定是连续的。具体的例子可以去查《分析中的反例》，或者很多数学分析教材上也会有。 连续函数的变上限积分一定是连续的（而且进一步的，一定是可导的）。

导数不一定连续。为了说明这一点，我们考虑一个具体的例子。假设函数定义为。我们首先证明这个函数处处可导。通过导数的定义，我们可以计算出在任何点处的导数存在。然而，当接近时，导数的极限并不存在，因此导数在处不连续。这说明，即使函数在开区间内可导，其导数也可能在某些点处不连续。

The End