拐点是点还是坐标（曲线的拐点是点还是坐标）

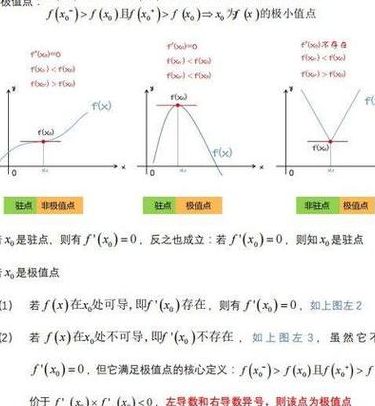
什么是驻点、极值点和拐点?

极值点、驻点、拐点是函数在不同情境下的特殊点，三者有着明确的区别。极值点指的是函数在整个定义域上最大或最小的点，即函数值达到最大或最小的那些点。这些点是函数的局部或全局的最优解。在极值点处，函数的导数等于零。

驻点、极值点和拐点都是函数在特定点的性质。驻点指的是函数在该点的一阶导数为0，可能是极值点，也可能不是。极值点则是指函数在该点取得极值，该点可能是驻点，也可能是其他类型的点。拐点则是指函数在该点的二阶导数为0，并且二阶导数的符号改变，该点可能是拐点，也可能是其他类型的点。

极值点、驻点与拐点：极值点：若f(a)是函数f(x)的极大值或极小值，则a为函数f(x)的极值点，极大值点与极小值点统称为极值点。极值点是函数图像的某段子区间内上极大值或者极小值点的横坐标。

驻点和零点是x，极值点和拐点是坐标（x，y）。我们把导数f(x)的零点（即方程f(x)=0的根）叫做函数的驻点，也称临界点、稳定点，驻点可能是函数的极值点，在“这一点”，函数的输出值停止增加或减少，对于一维函数的图像，驻点的切线平行于x轴，对于二维函数的图像，驻点的切平面平行于xy平面。

极值点是函数值在某点达到局部最大或最小值的点，它同样不是几何意义上的点。在导数存在的情况下，判断极值点需要关注二阶导数的符号变化：如果二阶导数存在，满足零点且两侧符号改变或恒为零；若二阶导不存在，就依赖于定义上的条件。

驻点的定义是函数在该点的一阶导数为0，而拐点则要求二阶导数为0。值得注意的是，二阶导数为0时，并不一定意味着一阶导数为0；同样，一阶导数为0时，二阶导数也不一定为0。这些特性使得驻点和拐点在函数的性质判断中扮演着不同的角色。

拐点是点还是坐标?

拐点、驻点、极值点都是指具体的点，而不是坐标。拐点是函数图像上凸凹性发生改变的点。在微积分中，拐点是函数图像上凸凹性发生改变的点，它标志着函数在该点处的弯曲方向发生了变化。

拐点是坐标。拐点是一个点，由横坐标和纵坐标组成，如点(a，b)。在连续曲线上，凹凸部分的分界点称为曲线的拐点。若某点同时满足以下两个条件，则可以判定为拐点：函数在该点处的二阶导数为0；在该点的左右两边的二阶导数异号。

拐点是函数图像上的一个特殊点，通常用坐标来表示。在数学中，拐点是指函数图像上的一个点，它两侧的曲线斜率发生变化的点。也可以说，拐点是函数曲线由凸转凹或由凹转凸的点。在几何意义上，拐点是函数图像上的一个转折点。

拐点是指曲线上的点。这点的位置当然要用坐标表示。拫据拐点的定义，当曲线经过这点时，曲线向上凹（向下凹）变成向下凹（向上凹）。它是个转折点。

拐点是点。拐点是数学用语，又称反曲点，是指在数学上指改变曲线向上或向下方向的点，拐点是导数符号发生变化的点，可以是相对最大值或相对最小值，如果函数是可微分的，那么拐点是一个固定点，但不是所有的固定点都是拐点。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号或不存在。

拐点,驻点,极值点分别是点还是极坐标

二是利用函数的性质，包括一阶导数和二阶导数等的性质，判断函数的单调性、奇偶性、周期性和凸性等，结合关键点，如极值点、最值点、拐点、零点、与y轴的交点等，画出函数的图像。最后一种方法是利用计算器软件画出函数图像。这当然是最省力的方法了。

在函数取得极值处，曲线上的切线是水平的，但曲线上有水平曲线的地方，函数不一定取得极值，即可导函数的极值点必定是它的驻点(导数为0的点)，但函数的驻点却不一定是极值点。

当球体为高阻(μ2=10)时，在球心正上方有ρS极大值，两侧有ρSρ1的极小值。无论高阻还是低阻球体，其上的视电阻率曲线皆左右对称。因此根据ρS曲线主极值点的坐标，可确定球心在地面的投影位置。 图4-14 主剖面上中梯法球体ρS曲线 视电阻率的变化特征反映了地下不均匀岩石中的电场分布情况。

平方 平方是一种运算，比如，a的平方表示a×a，简写成a，也可写成a×a(a的一次方乘a的一次方等于a的2次方），例如4×4=16，8×8=64，平方符号为2。立方 立方也叫三次方。三个相同的数相乘，叫做这个数的立方。如5×5×5叫做5的立方，记做5。

什么是拐点?

定义：拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即曲线的凹凸分界点）。意义：若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。二阶导数，是原函数导数的导数，将原函数进行二次求导。

拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。

拐点：又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点即曲线的凹凸分界点。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号或不存在。在生活中借指事物的发展趋势开始改变的地方。特别意义：在数学领域是指，凸曲线与凹曲线的连接点。

拐点是点还是坐标

拐点、驻点、极值点都是指具体的点，而不是坐标。拐点是函数图像上凸凹性发生改变的点。在微积分中，拐点是函数图像上凸凹性发生改变的点，它标志着函数在该点处的弯曲方向发生了变化。

拐点是坐标。拐点是一个点，由横坐标和纵坐标组成，如点(a，b)。在连续曲线上，凹凸部分的分界点称为曲线的拐点。若某点同时满足以下两个条件，则可以判定为拐点：函数在该点处的二阶导数为0；在该点的左右两边的二阶导数异号。

拐点，驻点均是指点，而极值点则是X轴上的横坐标。拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。

驻点、拐点、极值点、零点等点哪些是点(全部坐标),哪些是横坐标?

1、解驻点、极值点、零点等点都是指的是横坐标，都是x的值。

2、零点，驻点，极值点指的都是函数y=f(x)的一个横坐标x0，而拐点指的是函数y=f(x)图像上的一个点。拐点：二阶导数为零，且三阶导不为零；驻点：一阶导数为零或不存在。极值点：若f(a)是函数f(x)的极大值或极小值，则a为函数f(x)的极值点，极大值点与极小值点统称为极值点。

3、极值点，最值点，驻点，零点都指的是横坐标x 拐点指的是（x，y）坐标 拐点在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。

4、驻点是指横坐标。驻点，零点，极值点是横坐标，拐点是一个点，有横纵坐标，驻点是指使函数的一阶导数为0的那个x值，从图像看，驻点是一个点，其数值就是这个点的x坐标，比如f（3）=0，那么x=3就是一个驻点，在数轴上是一个点，这个点的坐标就是（3，0）。

5、极值点、驻点与拐点：极值点：若f(a)是函数f(x)的极大值或极小值，则a为函数f(x)的极值点，极大值点与极小值点统称为极值点。极值点是函数图像的某段子区间内上极大值或者极小值点的横坐标。

6、很负责地说：是横坐标。此外“点”是横坐标的还有：零点，驻点，极值点。

The End