椭圆第二定义（椭圆第二定义的证明）

椭圆第二定义公式

椭圆第二定义公式是：椭圆上的点P（X，Y）到左焦点F1的距离是d=a+ex，到右焦点的距离d=a-ex。椭圆（Ellipse）是平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。

椭圆第二定义公式：d/（a^2/c+x）=e。椭圆：在数学中，椭圆是围绕两个焦点的平面中的曲线，使得对于曲线上的每个点，到两个焦点的距离之和是恒定的。因此，它是圆的概括，其是具有两个焦点在相同位置处的特殊类型的椭圆。椭圆的形状由其偏心度表示，对于椭以是从0到任意接近但小于1的任何数字。

椭圆第二定义公式推导过程如下：推导过程：离心率e=c/a，其中c是焦点到椭圆中心的距离，a是椭圆的长半轴长度。可以根据椭圆的定义来推导这个公式。椭圆是平面上到两个固定点F1和F2的距离之和等于常数（大于｜F1F2|）的点的轨迹。

第一公式：把平面内与两个定点F1，F2的距离之和等于常数（大于│F1F2│）的点的轨迹叫做椭圆。这两个顶点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。第二公式：平面到顶点F（e，0)的距离到顶直线l；x=a^2/c的距离之比为e=c/a(a＞c＞0)的点的轨迹叫椭圆。

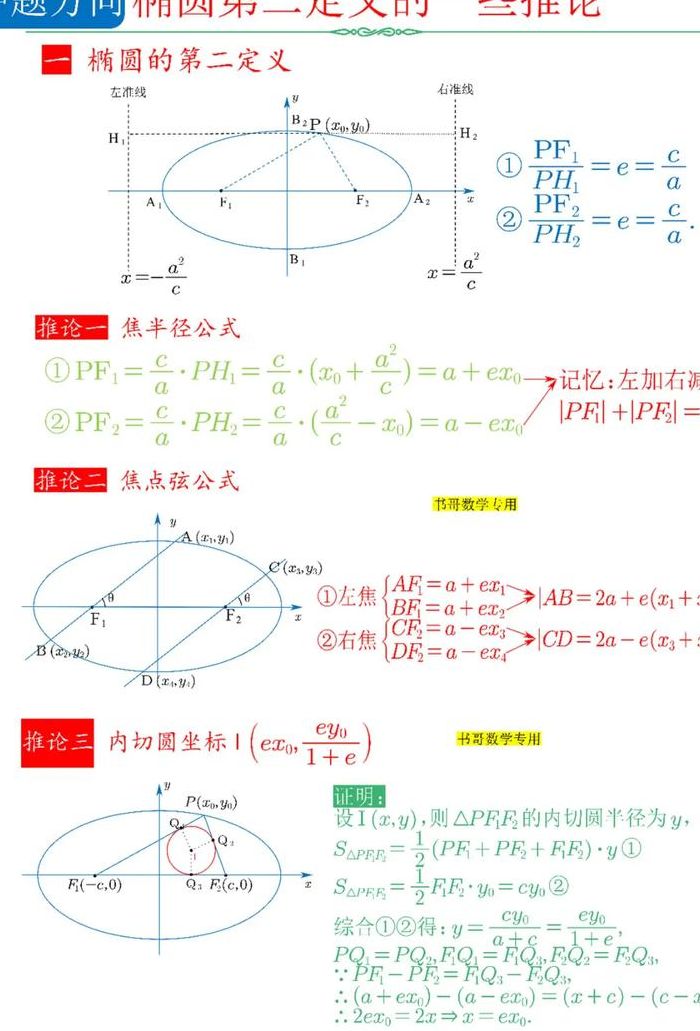
第二定义 平面上到定点F的距离与到定直线的距离之比为常数e(即椭圆的离心率，e=c/a)的点的集合（定点F不在定直线上，该常数为小于1的正数）其中定点F为椭圆的焦点，定直线称为椭圆的准线（该定直线的方程是x=±a^2/c焦点在X轴上或者y=±a^2/c焦点在Y轴上)。

椭圆焦半径公式 x=a+ex1 x2=a-ex1 椭圆过右焦点的半径r=a-ex 过左焦点的半径r=a+ex 双曲线定义：一动点移动于一个平面上，与平面上两个定点F1，F2的距离的差的绝对值始终为一定值2a(2a小于F1和F2之间的距离）时所成的轨迹叫做双曲线。两个定点F1，F2叫做双曲线的焦点。

椭圆的第二定义

第二定义 平面上到定点F的距离与到定直线的距离之比为常数e(即椭圆的离心率，e=c/a)的点的集合（定点F不在定直线上，该常数为小于1的正数）其中定点F为椭圆的焦点，定直线称为椭圆的准线（该定直线的方程是x=±a^2/c焦点在X轴上或者y=±a^2/c焦点在Y轴上)。

第二定义：平面上到定点距离与到定直线间距离之比为常数的点的集合。这个常数记为e，当e1时为双曲线了。

椭圆的第二定义是到一定点与一定直线的距离之比等于定值（这个定值小于1）的点的集合为一椭圆。椭圆的定义：椭圆（Ellipse）是平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。也可以这样定义椭圆，椭圆是点的集合，点其到两个焦点的距离的和是固定数。

关于椭圆的第一定义和第二定义

第一定义：平面内与两定点FF2的距离的和等于常数2a的动点P的轨迹叫做椭圆。第二定义：平面内到定点F的距离与到定直线的距离之比为常数e，其中定点F为椭圆的焦点，定直线称为椭圆的准线。

椭圆，是平面上到两个固定点的距离之和为常数的轨迹。这两个固定点被称为焦点。作为圆锥曲线的一种，椭圆是圆锥与平面的交线。其方程可以表达为标准形式：x/a + y/b = 1。根据第一定义，平面内与两定点FF2的距离之和等于常数2a的动点P的轨迹，被定义为椭圆。

椭圆，这个平面曲线家族的代表，其独特的性质在于其轨迹——任何点P沿着椭圆运动时，到两个固定点F1和F2的距离之和恒定，这个常数正是椭圆的半长轴的两倍，即2a。从这个第一定义出发，我们观察到椭圆的形状并非简单地圆，而是通过圆锥与平面的交线塑造的。然而，椭圆的第二定义为我们提供了另一种视角。

椭圆的第一定义，说的是“平面内到两个定点的距离之和等于定长的点的集合（轨迹）”，第二定义，说的是“平面内到一个定点（焦点）的距离和它到一条定直线（准线）的距离的比值等于常数的点的集合（轨迹）”。

椭圆第二定义：椭圆是圆锥曲线的一种，即圆锥与平面的截线。椭圆第三定义：椭圆的周长等于特定的正弦曲线在一个周期内的长度。在数学中，椭圆是围绕两个焦点的平面中的曲线，使得对于曲线上的每个点，到两个焦点的距离之和是恒定的。

The End