偏导数连续（偏导数连续几何解释图）

怎么判断函数的偏导连续呢?

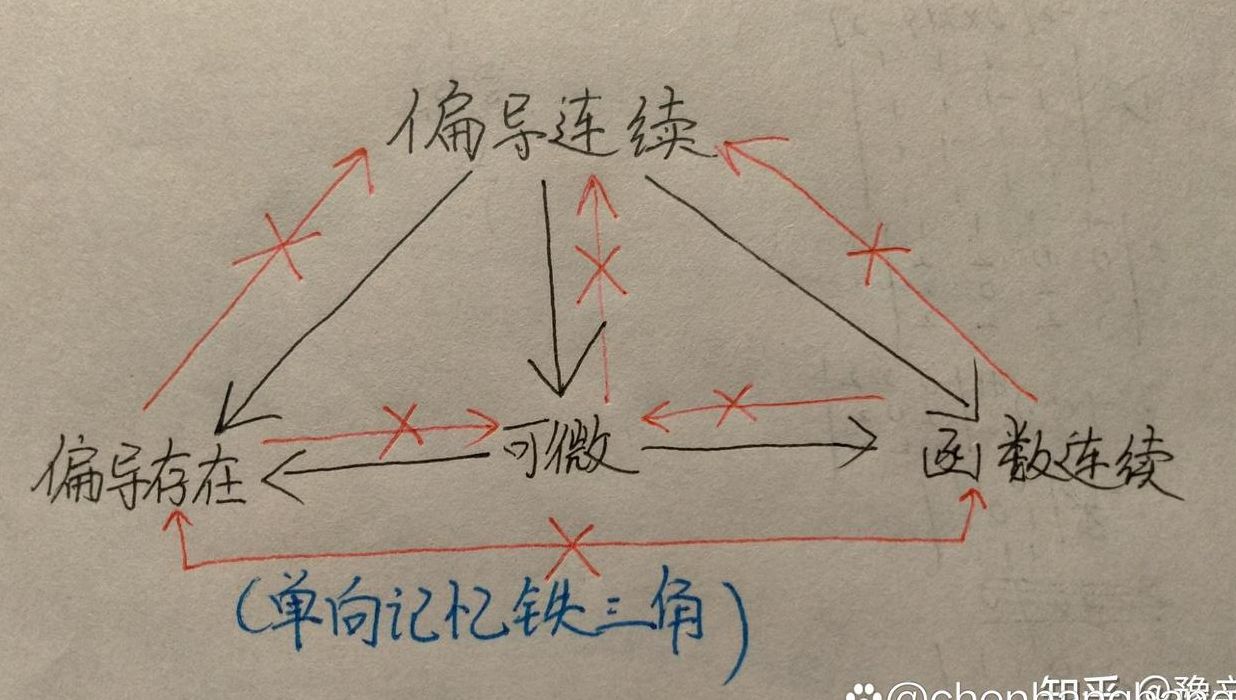
1、偏导数存在和偏导数连续的关系是：偏导数连续，则偏导数存在；但是，当偏导数存在时，偏导数不一定连续。偏导连续是偏导存在的充分条件；而偏导存在是偏导连续的必要条件。上图是偏导数存在与偏导连续之间的关系。偏导连续是指求出的偏导以后的函数是连续的。

2、先用定义求出该点的偏导数值c，再用求导公式求出不在该点时的偏导数fx(x，y)，最后求fx(，x，y)当(x，y)趋于该点时的极限，如果limfx(x，y)=c，即偏导数连续，否则不连续。

3、首先确定偏导数是否存在。 对偏导数进行连续性的判断。 如果偏导数均存在且均连续，则原函数可偏导。 举例说明如何判断偏导数连续 下面举例说明如何判断偏导数的连续性。对于函数 f(x，y)=x^3y^2，在区域内(x，y)∈R2，求其偏导数连续性。

4、问题一：怎么判断这道题的偏导数是否存在，是否连续？连续是要在点（0，0）的一个邻域内所有值都相等，当以直线Y=KX靠近时，显然与K值有关，所以不连续。对X的偏导存在只需在X轴方向上邻域内的值相等就行，所以存在。对Y同理。

偏导数连续的条件

1、偏导数在某点连续的条件是指该函数在该点的偏导数不仅存在，而且其变化趋势是平滑的，没有突变。对于一元函数而言，如果其导数在某点存在且连续，则该函数在该点是可导的。同样地，对于多元函数而言，如果其偏导数在某点存在且连续，则该函数在该点是可偏导的。

2、首先，根据偏导数的定义，求出函数在某一点的偏导数值。然后，检查该点的邻域内的函数值，确保它们都在定义域内。如果函数在某一点的偏导数值存在且连续，则该函数的偏导数在该点连续。如果函数在所有点的偏导数都连续，则该函数的偏导数在整个定义域内连续。

3、连续是偏导数存在的充分不必要条件，即偏导数存在且连续则函数可微，而函数可微推不出偏导数存在且连续。偏导数fx（x0，y0）表示固定面上一点对x轴的切线斜率；偏导数fy（x0，y0）表示固定面上一点对y轴的切线斜率。

4、f(x，y)=x+2y 对x的偏导是1，对y的偏导是2 。

5、偏导数存在和偏导数连续的关系是：偏导数连续，则偏导数存在；但是，当偏导数存在时，偏导数不一定连续。偏导连续是偏导存在的充分条件；而偏导存在是偏导连续的必要条件。上图是偏导数存在与偏导连续之间的关系。偏导连续是指求出的偏导以后的函数是连续的。

偏导数连续怎么证明

1、偏导数连续的证明方法是基于偏导数的定义与极限理论。首先，通过偏导数的定义计算出给定点的偏导数值c。然后，使用求导公式找到不在该点时的偏导数fx(x，y)。接着，求解fx(x，y)在(x，y)趋于给定点时的极限。

2、偏导数连续证明方法：先用定义求出该点的偏导数值c，再用求导公式求出不在该点时的偏导数fx(x，y)，最后求fx(，x，y)当(x，y)趋于该点时的极限，如果limfx(x，y)=c，即偏导数连续，否则不连续。

3、偏导数连续证明方法包括三个步骤：首先，通过定义求出该点的偏导数值c。接着，运用求导公式求出不在该点的偏导数fx(x，y)。最后，求解fx(，x，y)当(x，y)趋向该点的极限，若limfx(x，y)=c，则偏导数连续；否则，偏导数不连续。

4、在数学分析中，证明偏导数连续的方法可以通过一系列步骤完成。首先，我们需要利用偏导数的定义求出给定点的偏导数值c。具体而言，我们可以通过对函数沿x轴或y轴的偏导数定义进行计算，得到该点处的偏导数值c。

5、第一步，定义 f(x， y) 在 (a， b) 对 x 的偏导数为 f_x(a， b) = lim(h-0) [f(a+h， b) - f(a， b)] / h。接着，定义 f(x， y) 在 (a， b) 对 y 的偏导数为 f_y(a， b) = lim(k-0) [f(a， b+k) - f(a， b)] / k。

6、怎么证明偏导数连续如下：先用定义求出该点的偏导数值c，再用求导公式求出不在该点时的偏导数fx（x，y），最后求fxx，y当x，y趋于该点时的极限，如果limfx（x，y）=c，即偏导数连续，否则不连续。

偏导函数在(x,y)连续到底什么意思啊

1、简单来说，偏导数的连续性是确保函数在某点的微分性质的关键。这种连续性不仅保证了在各个方向上的导数存在，还确保了函数在该点的微分性质。而方向导数的概念，可以帮助我们更好地理解函数在不同方向上的变化率，进而通过矢量合成的方式，将各个方向的导数综合起来，得到函数在该点的全面性质。

2、偏导数连续，通过矢量合成，就得到所有方向的方向导数存在；既然所有方向的方向导数存在，就是所有方向可导，就是可微。就这么简单。

3、偏导数存在且连续（这个连续指的是求完偏导的函数）=可微，反之推不出；可微=偏导数存在，反之推不出；可微=连续（这个连续指的是没求偏导的函数），反之推不出；可微=方向导数存在，反之推不出；偏导数存在，连续，方向导数存在之间互相谁也推不出谁。

为什么偏导数连续就可微分

1、如果偏导数在该点连续，这样的线性函数(L(x， y))确实存在，满足了可微性的定义。因此，偏导数的连续性是函数可微的关键。但是，值得注意的是，偏导数连续并不是函数可微的唯一条件。即使偏导数在某点连续，函数在该点也未必可微。可微性还需满足其他条件，例如偏导数的存在性。

2、偏导数连续是可微分充分条件，但不是必要条件。比如下面这个函数f(x，y)，函数的表达式为当x，y均为有理数时f(x，y)=x^2+y^2；当x，y中有一个变量为无理数时f(x，y)=0。

3、偏导数连续是可微分的充分条件，但不是必要条件。比如，考虑一个函数f(x，y)，其定义为：当x和y均为有理数时，f(x，y)=x^2+y^2；而当x或y中有一个为无理数时，f(x，y)=0。这个函数在点(0，0)处的微分情况值得注意。

4、偏导数连续是函数可微的充分条件。 偏导数连续意味着函数在某点的局部行为可以通过一个线性逼近来近似描述。 对于多元函数，偏导数连续性是判断函数可微性的一个重要条件。 偏导数定义为函数在固定其他自变量的情况下，对单一自变量的变化率。

5、这是因为偏导数仅描述了函数在特定方向上的变化率，它对于函数在某一点附近整体变化情况的描述是不完整的。偏导数的存在并不能充分揭示函数在某点的局部行为，这限制了偏导数作为函数可微性判断的唯一标准。

The End