三角形的重心（三角形的重心在哪）

三角形的重心公式是什么?

1、答案：三角形的重心公式是：对于三角形ABC，其重心G的坐标可以通过以下公式计算：Gx=/3，Gy=/3。这里的x和y是三角形各个顶点的横纵坐标。当三个顶点在同一条直线上时，重心就在该直线上距离端点三分之一处。此外，三角形重心到三角形三个顶点的距离之和最小。重心是三角形的一个重要特征点。

2、重心坐标公式推导是AB中点横坐标为（x1+x2）/2，重心在中线距AB中点1/3处，故重心横坐标为xm=1/3×{x3-（x1+x2）/2}+（x1+x2）/2=（x1+x2+x3）/3。同理，ym=（y1+y2+y3）/3。重心坐标定义：三角形所在平面的任意点都能表示为顶点的加权平均值，这个权就叫做重心坐标。

3、三角形重心公式是三角形的重心G的坐标是A+B+C除于3。内容如下：重心是指地球对物体中每一微小部分引力的合力作用点。

三角形的重心是什么?

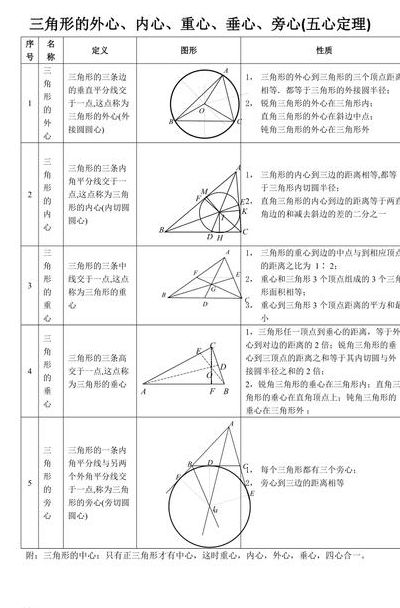
1、三角形的重心是三角形的三条中线交于一点。三角形的五心定理 重心定理：三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍。该点叫做三角形的重心。外心定理：三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。垂心定理：三角形的三条高交于一点。该点叫做三角形的垂心。

2、三角形的重心是指三角形三条边的中点所连成的线段交点。这个交点就是三角形的重心。接下来详细解释三角形的重心这一概念：三角形重心的定义 在三角形中，重心是一个特殊的点。它是三角形三条边的中点所连成的三条线段。这个点的存在对于理解三角形的几何特性非常重要。

3、三角形的重心是指三角形内所有三个顶点的平均位置，也可以被视为三角形的质心或几何中心。重心具有以下特点：位置：重心位于三角形的三条中线的交点处，每条中线连接一个顶点和对边中点。重心离三角形的各个顶点的距离是相等的，这是三角形的平衡点。

三角形的重心

1、三角形的重心是三角形三边中点的交点。简单说，就是三条中线相交于一点，这一点就是三角形的重心。重心是三角形的一个重要特征点，具有独特的几何性质。重心性质 三角形的重心具有许多重要性质。

2、三角形的重心是三角形的三条中线交于一点。三角形的五心定理 重心定理：三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍。该点叫做三角形的重心。外心定理：三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。垂心定理：三角形的三条高交于一点。该点叫做三角形的垂心。

3、三角形的重心是三角形三条中线的交点.三角形的重心到顶点的距离等于到对边中点距离的2北.在直角坐标系内，若三顶点的坐标分别为(x1，y1)，(x2，y2)，(x3，y3)，则三角形的重心G的坐标为((x1+x2+x3)/3，(y1+y2+y3)/3).三角形的重心是到三角形三顶点距离的平方和最小的点。

4、三角形的中心：仅当三角形是正三角形的时候，重心、垂心、内心、外心四心合一心，这个心是三角形的中心。三角形重心：三角形三条中线的交点即为三角形重心。性质：重心到顶点的距离与重心到对边中点的距离之比为2：1。重心和三角形3个顶点组成的3个三角形面积相等。

三角形的重心的公式

1、答案：三角形的重心公式是：对于三角形ABC，其重心G的坐标可以通过以下公式计算：Gx=/3，Gy=/3。这里的x和y是三角形各个顶点的横纵坐标。当三个顶点在同一条直线上时，重心就在该直线上距离端点三分之一处。此外，三角形重心到三角形三个顶点的距离之和最小。重心是三角形的一个重要特征点。

2、重心坐标公式推导是AB中点横坐标为（x1+x2）/2，重心在中线距AB中点1/3处，故重心横坐标为xm=1/3×{x3-（x1+x2）/2}+（x1+x2）/2=（x1+x2+x3）/3。同理，ym=（y1+y2+y3）/3。重心坐标定义：三角形所在平面的任意点都能表示为顶点的加权平均值，这个权就叫做重心坐标。

3、三角形重心公式：x=（x1+x2+x3）/3。三角形是由三条线段相交而成的平面图形，重心是三角形内部一个特殊的点，它是三角形三条中线的交点，也是三角形重心定理的一个重要应用。在三角形的许多问题中，重心都是一个重要的概念。

4、三角形重心公式是三角形的重心G的坐标是A+B+C除于3。内容如下：重心是指地球对物体中每一微小部分引力的合力作用点。

5、三角形的重心：三角形的三条中线相交于一点，这点叫做三角形的重心。重心到各边中点的距离，等于这边上中线的三分之一。

6、重心公式是P=w1*P1+w2*P2+w3*P3。数学上的重心是指三角形的三条中线的交点，其证明定理有燕尾定理或塞瓦定理，应用定理有梅涅劳斯定理、塞瓦定理。重心的几条性质：重心到顶点的距离与重心到对边中点的距离之比为2：1。重心和三角形3个顶点组成的3个三角形面积相等。

三角形的重心是哪个?

1、三角形重心是三角形内部的一个特殊点。它是三条从顶点出发，穿过相对边中点的线段的交点。也可以说，重心是三角形三条边的中点连线的交点。几何性质 重心具有许多重要的几何性质。例如，从重心出发，到三角形的每个顶点的线段，与相应的中线之间的比例是固定的，即等于该中线的两倍长度。

2、三角形的中心：仅当三角形是正三角形的时候，重心、垂心、内心、外心四心合一心，这个心是三角形的中心。三角形重心：三角形三条中线的交点即为三角形重心。性质：重心到顶点的距离与重心到对边中点的距离之比为2：1。重心和三角形3个顶点组成的3个三角形面积相等。

3、重心：三角形三中线的交点，叫重心。性质：重心分中线两段的比为2/1。内心：三角形三内角平分线的交点，叫内心。即三角形内切圆的圆心。性质：内心到三角形三边的距离相等。外心：三边垂直平分线交点。即三角形外接圆的圆心。性质：外心到三个顶点距离相等。垂心：三高的交点。

4、三角形的重心是指三角形三条中线的交点，它被称为重心或质心。三角形的重心的重要性质 重心到三个顶点的距离相等：从重心到三个顶点的距离相等，即重心到每条边的中点的距离相等。三个重心到对边中点的线段交于一点：连接重心和三个对边中点的线段交于一点，这个点即为重心。

5、任何三角形的重心是指这个三角形三条中线的交点；因为三角形重心是三角形三条中线的交点，故而肯定在斜边的中线上，而对于等腰三角形而言，重心就是斜边中线的中点，两点相交。有关三角形重心的性质：重心到顶点的距离与重心到对边中点的距离之比为2：1。

6、三角形的中心：仅当三角形是正三角形的时候，重心、垂心、内心、外心四心合一心，称做正三角形的中心。三角形的重心：三条中线的交点，这点到顶点的距离是它到对边中点距离的2倍。重心分中线比为1：2。三角形的内心：三条角平分线的交点，是三角形的内切圆的圆心的简称。到三边距离相等。

The End