三角形的外接圆（三角形的外接圆怎么画）

三角形的外接圆有什么性质

1、三角形外接圆的性质有：三角形外接圆的圆心是三角形外心，外心到三角形三个顶点的距离相等。三角形外接圆的半径是三角形外心到任意一个顶点的距离。三角形内心、垂心、重心和外心四个点共圆，即在三角形外接圆上。

2、三角形外接圆的性质有哪些如下：性质1：锐角三角形的外心在三角形内；直角三角形的外心在斜边上，与斜边中点重合；钝角三角形的外心在三角形外.等边三角形外心与内心为同一点。性质2：∠BGC=2∠A。性质3：∠GAC+∠B=90°。

3、外接圆的性质如下：锐角三角形外心在三角形内部。直角三角形外心在三角形斜边中点。钝角三角形外心在三角形外。有外心的图形，一定有外接圆（各边中垂线的交点，叫做外心）。外接圆圆心到三角形各个顶点的线段长度相等。

三角形的外接圆怎么画?

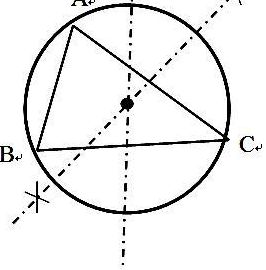
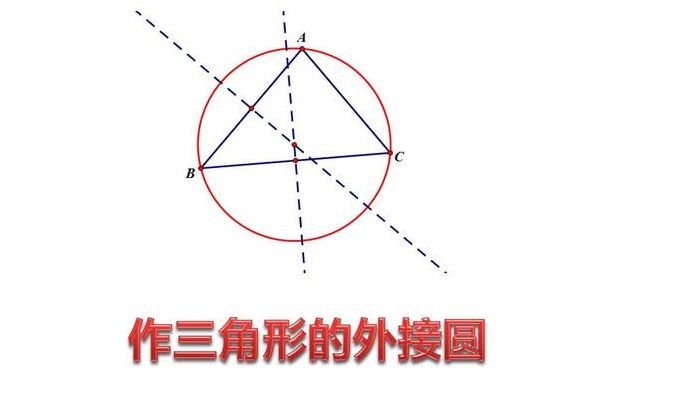
1、以三角形ABC为例：作线段AB的垂直平分线L。作线段BC的垂直平分线与直线L交于O。以点O为圆心，以OA的长为半径作圆即可。做其中两条边条边的垂直平分线，以此交点为圆心。分别以线段两端为圆心，以大于线段1/2为半径在线段两侧作弧，连两相交点，此线就是该线段的垂直平分线。

2、步骤1，画△ABC边AB的垂直平分线DE，如下图：步骤画△ABC边BC的垂直平分线FG，交DE与H，如下图：步骤H就是外接圆的圆心，以H为圆心，以HA为半径画圆H，圆H就是三角形ABC的外接圆，如下图：圆H就是三角形ABC的外接圆。

3、用圆规作等边三角形的外接圆：如图，在等边三角形任意两边各作一条垂直平分线，两条垂直平分线的交点就是外接圆圆心，这时以该交点和三角形任意一角的连线为半径作圆，即为该三角形的外接圆。

4、解答过程：设圆的一般方程为x^2+y^2+Dx+Ey+F=0。由该圆过已知三角形的三个顶点，将三个顶点坐标代入圆的一般方程。得到关于D，E，F的三元一次方程组，解得D，E，F即可。与多边形各顶点都相交的圆叫做多边形的外接圆。三角形有外接圆，其他的图形不一定有外接圆。

5、第一步：任意做一条垂直于直径AB的直线。原理是直径上的圆周角为直角以及三角形三条高线交于一点。如左上图，步骤略过。第二步：做出垂直于直径AB的直径。（这也就做出了圆内接正方形）利用直径的中点是圆心。不断利用平行和中点，很容易做出，如右上图。步骤略过。

6、先画出任意两边的垂直平分线，它们的交点就是这个三角形的外接圆的圆心，然后以这个点到三角形的任一个顶点的线段长为半径，作出来的圆就是这个三角形的外接圆。

三角形的外接圆和内切圆有什么区别和联系

1、三角形的外接圆：圆与三角形的三个顶点相交。圆心是三条边的中垂线交点。如下图：内切圆（注意叫内切哦）：圆与三角形的三条边相交。圆心是三个内角的角平分线交点。如下图：三角形外接圆 定义 与三角形三个顶点都相交的圆叫做三角形的外接圆。三角形的外接圆圆心是任意两边的垂直平分线的交点。

2、半径关系：内切圆的半径等于三角形周长与半周长的差的一半，而外接圆的半径等于三角形周长的一半。圆心关系：三角形的内心、外心、垂心、重心都与内切圆和外接圆相关。其中，内心是三角形三个内角平分线的交点，外心是三条边的垂直平分线的交点，垂心是三条高的交点，重心是三条中线的交点。

3、我认为内切圆和外接圆的区别如下定义。外接圆：与多边形各顶点都相交的圆叫做多边形的外接圆。内切圆：在数学中，若一个二维平面上的多边形的每条边都能与其内部的一个圆形相切，该圆就是多边形的内切圆。作图方法。

4、三角形外接圆的圆心叫做这个三角形的外心，这个三角形叫做这个圆的内接三角形，外心是三角形各边中垂线的交点；直角三角形外接圆半径等于斜边的一半。与三角形各边都相切的圆叫做三角形的内切圆。

5、如下：①三角形的外接圆有关定理：三角形各边垂直平分线的交点，是外心。外心到三角形各顶点的距离相等。外心到三角形各边的垂线平分各边。② 三角形的内切圆有关定理：三角形各内角平分线的交点，是内心。内心到三角形各边的距离相等。三角形任一顶点到内切圆的两切线长相等。

6、三角形的外接圆定理：（1）三角形各边垂直平分线的交点，是外心。（2）外心到三角形各顶点的距离相等。（3）外心到三角形各边的垂线平分各边。三角形的内切圆定理：（1）三角形各内角平分线的交点，是内心。（2）内心到三角形各边的距离相等。

The End