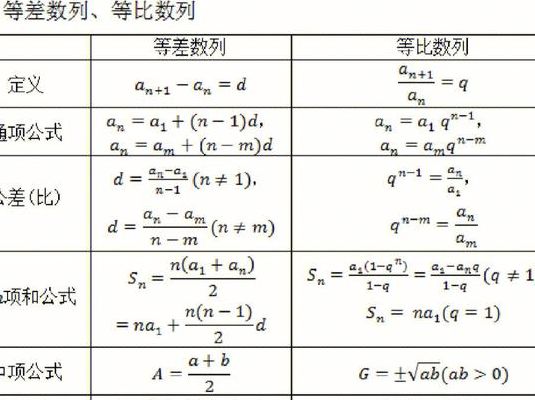
等差数列所有公式（等和数列的公式）

等差数列公式

等差数列公式一般项公式：an=a1+(n-1)d。和公式：Sn=n(a1+an)/2。等比数列的一般项公式：an=a1*q^(n-1)。等比数列的和公式：Sn=a1*(1-q^n)/(1-q)。等比级数的和公式：S=a1/(1-q)。三项和公式：Sn=a1+an+an-1。

等差数列的求和公式：Sn= n/2*（a1+an），其中Sn是前n项和，a1是第一项，an是第n项。等差数列的项数公式：项数n=（an- a1）/d+1，其中an是第n项，a1是第一项，d是公差。等差数列的公差公式：d=（an- a1）/（n-1），其中an是第n项，a1是第一项，d是公差。

等差数列公式：an=a1+(n-1)d，（n为正整数）a1为首项，an为第n项的通项公式，d为公差。

- 项数 = (末项 - 首项) ÷ 公差 + 1 - 首项 = 末项 - (项数 - 1) * 公差 - 和 = (首项 + 末项) * 项数 ÷ 2 其中，末项是数列中的最后一项，首项是数列中的第一项，项数表示数列中数字的个数，和是数列所有数字的总和。

公差，公差常用字母 d表示。等差数列的通项公式为：an=a1+(n-1)d (1)前n项和公式为：Sn=na1+n(n-1)d/2或Sn=n(a1+an)/2 (2)以上n均属于正整数。

请问等差数列公式有哪些?

一般项公式：an=a1+(n-1)d。和公式：Sn=n(a1+an)/2。等比数列的一般项公式：an=a1*q^(n-1)。等比数列的和公式：Sn=a1*(1-q^n)/(1-q)。等比级数的和公式：S=a1/(1-q)。三项和公式：Sn=a1+an+an-1。

等差数列的通项公式为：an=a1+(n-1)d (1)前n项和公式前n项和公式为：Sn=na1+n(n-1)d/2或Sn=n(a1+an)/2 (2)以上n均属于正整数。

- 首项 = 末项 - (项数 - 1) * 公差 - 和 = (首项 + 末项) * 项数 ÷ 2 其中，末项是数列中的最后一项，首项是数列中的第一项，项数表示数列中数字的个数，和是数列所有数字的总和。

等差数列的公式包括：通项公式：an=a1+d 前n项和公式：Sn=n/2[2a1+d]或Sn=n/2。也可以写作等差数列求和公式Sn=*n^2+*n。其中第一项公式描述了数列中任意一项的值，第二项公式描述了数列前n项的和。等差数列的和与项数之间的关系通过这些公式可以得到精确的量化描述。

等差数列所有公式

1、一般项公式：an=a1+(n-1)d。和公式：Sn=n(a1+an)/2。等比数列的一般项公式：an=a1*q^(n-1)。等比数列的和公式：Sn=a1*(1-q^n)/(1-q)。等比级数的和公式：S=a1/(1-q)。三项和公式：Sn=a1+an+an-1。

2、等差数列的求和公式：Sn= n/2*（a1+an），其中Sn是前n项和，a1是第一项，an是第n项。等差数列的项数公式：项数n=（an- a1）/d+1，其中an是第n项，a1是第一项，d是公差。等差数列的公差公式：d=（an- a1）/（n-1），其中an是第n项，a1是第一项，d是公差。

3、等差数列的通项公式为：an=a1+(n-1)d (1)前n项和公式为：Sn=na1+n(n-1)d/2或Sn=n(a1+an)/2 (2)以上n均属于正整数。

4、等差数列的各种公式如下：项数公式：an = a1 + d 通项公式：an = am +d 或 an = a +d，其中 a 为首项，d 为公差。该公式描述了数列中的每一项与首项和公差之间的关系。前n项和公式：Sn = n/2 × [2a1 + d]，这是一个用来计算数列前n项和的公式。它也包含了首项a1和公差d。

5、等差数列{an}的通项公式为an=a1+(n-1)d。等差数列求和公式有①等差数列公式an=a1+(n-1)d、②前n项和公式为：Sn=na1+n(n-1)d/③若公差d=1时：Sn=(a1+an)n/④若m+n=p+q则：存在am+an=ap+aq、⑤若m+n=2p则：am+an=2ap，以上n均为正整数。

6、最后需要注意在等差数列中所有的奇数项和偶数项都可以构成新的等差数列。通过寻找和利用这些子数列的性质和规律可以简化解题过程并帮助记忆相关公式。另外还需记住在等差数列中从第一项开始每次跨越相同的项数其和的差值也呈现一定的规律。

The End