向量的方向余弦怎么求（向量的方向余弦计算公式）

向量的方向余弦

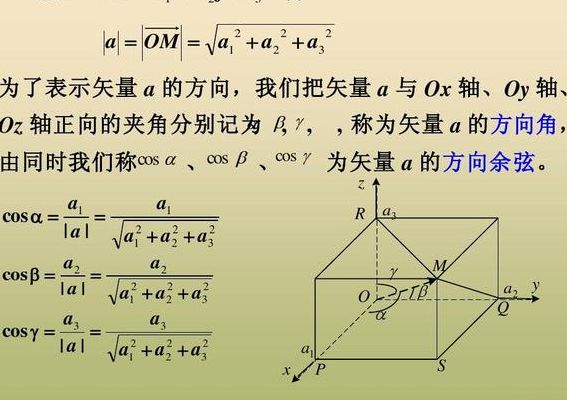
在数学中，向量MN={x，y，z}的单位向量可通过将向量MN除以其模得到，即单位向量为MN/|MN|。其中α、β、γ为方向角，方向余弦分别为cosα、cosβ、cosγ。具体而言，方向余弦可以通过坐标值除以向量的模来计算，即cosα=x/|MN|，cosβ=y/|MN|，cosγ=z/|MN|。

向量的方向余弦是向量在三维空间中的重要概念，它描述了向量与坐标轴之间的关系。

向量的方向余弦方向角，这是空间向量的一个基本概念问题。设向量a={x，y，z}，向量a°是向量a的单位向量， |a°|=1。则 a°=(cosα)i+(cosβ)j+(cosγ)k， 式中，i，j，k 是坐标单位向量；式中，α，β，γ就叫做向量的方向角；cosα，cosβ，cosγ就叫做方向余弦。

向量的方向余弦可以通过以下步骤求解： 选择向量坐标轴：选择一个坐标系，以向量起点为原点，以向量方向为坐标轴正方向。 计算向量在各个坐标轴上的分量：根据选择的坐标系，计算向量在x轴、y轴和z轴上的分量。 计算方向余弦：方向余弦是指向量与坐标轴之间的夹角的余弦值。

向量的方向余弦怎么求

1、向量的方向余弦可以通过以下步骤求解： 选择向量坐标轴：选择一个坐标系，以向量起点为原点，以向量方向为坐标轴正方向。 计算向量在各个坐标轴上的分量：根据选择的坐标系，计算向量在x轴、y轴和z轴上的分量。 计算方向余弦：方向余弦是指向量与坐标轴之间的夹角的余弦值。

2、在数学中，向量MN={x，y，z}的单位向量可通过将向量MN除以其模得到，即单位向量为MN/|MN|。其中α、β、γ为方向角，方向余弦分别为cosα、cosβ、cosγ。具体而言，方向余弦可以通过坐标值除以向量的模来计算，即cosα=x/|MN|，cosβ=y/|MN|，cosγ=z/|MN|。

3、向量的方向余弦用公式a=(cosα)i+(cosβ)j+(cosγ)k求得。方向余弦是一个向量的三个方向余弦分别是向量与三个坐标轴之间角度的余弦。两个向量之间方向余弦指的是这两个向量之间角度的余弦。另外方向余弦矩阵是由两组不同的标准正交基的基底向量之间的方向余弦所形成的矩阵。

4、向量的方向余弦计算公式：a°=(cosα)i+(cosβ)j+(cosγ)k。余弦（余弦函数），三角函数的一种。在Rt△ABC（直角三角形）中，∠C=90°，∠A的余弦是它的邻边比三角形的斜边，即cosA=b/c，也可写为cosa=AC/AB。余弦函数：f(x)=cosx（x∈R）。

5、设向量a={x，y，z}， 向量a°是向量a的单位向量， |a°|=1；则 a°=(cosα)i+(cosβ)j+(cosγ)k， 式中，i，j，k 是坐标单位向量；式中，α，β，γ就叫做向量的方向角；cosα，cosβ，cosγ就叫做方向余弦。

6、方向余弦的实质是向量与坐标轴夹角的余弦值，它在解析几何中起着桥梁作用，用于表达两个向量之间的角度关系，以及不同标准正交基之间的转换。例如，通过方向余弦矩阵，我们可以理解一组标准正交基相对于另一组的旋转或方向变换。

已知方向向量,如何求方向余弦?

在数学中，向量MN={x，y，z}的单位向量可通过将向量MN除以其模得到，即单位向量为MN/|MN|。其中α、β、γ为方向角，方向余弦分别为cosα、cosβ、cosγ。具体而言，方向余弦可以通过坐标值除以向量的模来计算，即cosα=x/|MN|，cosβ=y/|MN|，cosγ=z/|MN|。

向量的方向余弦可以通过以下步骤求解： 选择向量坐标轴：选择一个坐标系，以向量起点为原点，以向量方向为坐标轴正方向。 计算向量在各个坐标轴上的分量：根据选择的坐标系，计算向量在x轴、y轴和z轴上的分量。 计算方向余弦：方向余弦是指向量与坐标轴之间的夹角的余弦值。

若有向量MN={x，y，z}，则向量MN的单位向量就为向量MN除以向量MN的模，α、β、γ分别为方向角，方向余弦分别为cosα、cosβ、cosγ。而方向余弦即为cosα=x/|MN|，cosβ=y/|MN|，cosγ=z/|MN|。

两个向量之间方向余弦指的是这两个向量之间角度的余弦。另外方向余弦矩阵是由两组不同的标准正交基的基底向量之间的方向余弦所形成的矩阵。方向余弦矩阵可以用来表达一组标准正交基与另一组标准正交基之间的关系，也可以用来表达一个向量对于另一组标准正交基的方向余弦。

The End