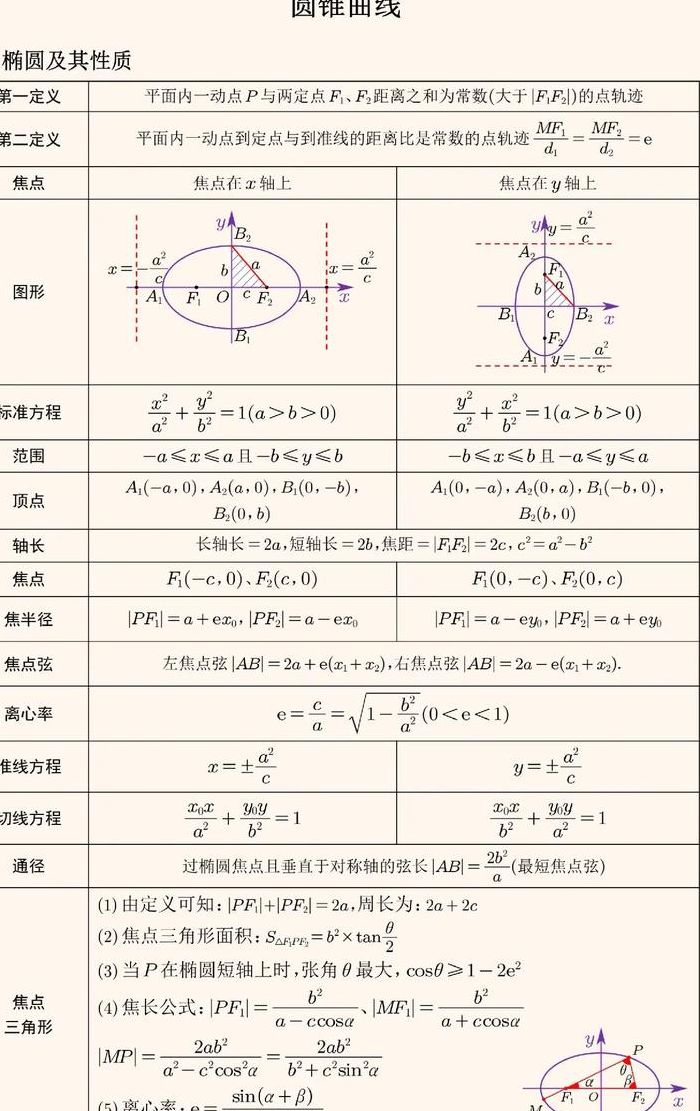
如何求切线方程与法线方程
切线方程:对函数求导(导函数为y=2x+3),然后求出在x=1时的导数y,此时y的值为经过x=1时的切线的斜率(根据导数的几何意义),知道切线的斜率了,然后再知道一个点的坐标就可以求出。
接下来,确定切线方程。切线在\(x=0\)时的斜率为2,因此切线方程为\(y=2x+1\),即切线通过点\((0,1)\)且斜率为2。法线与切线垂直,其斜率为切线斜率的负倒数。故法线的斜率为\(-\frac{1}{2}\)。
根据点斜式公式,我们可以写出切线方程:y=k(x-x0)+y0=f′(x0)*(x-x0)+f(x0)。同样地,法线方程也可以表示为:y=(-1/k)(x-x0)+y0=(-1/f′(x0))*(x-x0)+f(x0)。最后,根据具体需求,可以将这些方程进一步化简为一般式或斜截式。
法线方程与切线方程关系
切线方程和法线方程的关系是相互垂直,公共点是切点,过切点与切线垂直的直线为法线。记曲线为y=f(x)则在点(a,f(a))处的切线方程为:y=f(a)(x-a)+f(a),法线方程公式:α*β=-1。由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。
这两个方程的关系如下:法线方程是切线方程的垂线:在平面直角坐标系中,曲线上某一点的法线方程是该点的切线方程的垂线。切线方程是法线方程的垂线:在平面直角坐标系中,曲线上某一点的切线方程是该点的法线方程的垂线。
两者是垂直的关系。可以通过它们的斜率来理解。对于曲线y=f(x),在点(a,f(a))处的切线方程为y-f(a)=f(a)(x-a),其中f(a)表示曲线在点(a,f(a))处的切线斜率。法线方程的公式为y-f(a)=-1/f(a)(x-a),其中-1/f(a)表示法线的斜率。
切线方程和法线方程的关系是相互垂直。切线与法线的定义 切线 切线是曲线或曲面上的一条直线,且与给定点处的曲线或曲面切于一点。在二维平面上,切线与曲线仅有一个交点;而在三维空间中,切线可以经过曲线或曲面上的多个点。切线表示了曲线或曲面在给定点处的局部方向和变化率。
切线方程和法线方程怎么求
1、切线方程:对函数求导(导函数为y=2x+3),然后求出在x=1时的导数y,此时y的值为经过x=1时的切线的斜率(根据导数的几何意义),知道切线的斜率了,然后再知道一个点的坐标就可以求出。
2、函数图形在某点(a,b)的切线方程y=kx+b,先求斜率k,等于该点函数的导数值,再用该点的坐标值代入求b,切线方程求毕。法线方程:y=mx+c,m=-1/k,k为切线斜率,再把切点坐标代入求得c,法线方程求毕。切线方程是研究切线以及切线的斜率方程,涉及几何、代数、物理向量、量子力学等内容。
3、法线方程和切线方程是数学几何中常见的概念,法线方程通常写作y=f(a)(x-a)+f(a),其中f(a)是函数f在点a处的导数,f(a)是函数f在点a处的函数值。切线方程则通常表示为y=f(a)(x-a)+f(a),这个公式实际上与法线方程相同,但其应用范围不同。
4、法线和切线方程公式是y=f(a)(x-a)+f(a)和α*β=-1。法线是指始终垂直于某平面的虚线。在数学几何中法线指平面上垂直于曲线在某点的切线的一条线。几何上,切线指的是一条刚好触碰到曲线上某一点的直线。在物理学中过入射点垂直于镜面的直线叫做法线。
5、切线方程:y-y1=f(x1)(x-x1)法线方程:y-y1=(x1-x)/f(x1)当f(x)=e^x时,f‘(x)=e^x。
法线方程,切线方程的公理是什么?
公理包括:如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线;平行于同一条直线的两条直线平行。
截矩式:不适用于和任意坐标轴垂直的直线 知道直线与x轴交于(a,0),与y轴交于(0,b),则直线可表示为 bx+ay-ab=0 特别地,当ab均不为0时,斜截式可写为x/a+y/b=1 两点式:过(x1,y1)(x2,y2)的直线 (y-y1)/(y1-y2)=(x-x1)/(x1-x2)(斜率k需存在)。
直线的方向可以用与之平行的非零向量表示,称为方向向量,直线的位置则由经过的点和方向向量共同确定。在欧几里得几何中,直线的概念是直观的,其定义依赖于公理体系。在非欧几何中,直线是指连接两点间最短的线,即短程线。
公理(axiom):数学系统的基本假设,它可以推导出定理;例如:这系统可以是平面上的点与直线,则公理可以是「平面上任意二个相异点,存在唯一直线穿过这二点」。二项式(binomial):由二个单项式(monomial)的和或差所组成的代数式(关於单项式,请参阅单项式的定义)。例如:4a-8b。
由它经过的空间一点及它的一个方向向量完全确定。在欧几里得几何学中,直线只是一个直观的几何对象。在建立欧几里得几何学的公理体系时,直线与点、平面等都是不加定义的,它们之间的关系则由所给公理刻画。在非欧几何中直线指连接两点间最短的线,又称短程线。
切线方程和法线方程的求法是什么
在解析几何中,切线方程和法线方程是基础概念。考虑函数\(f(x)=x^3+kx+1\),其导数为\(f(x)=3x^2+2k\)。已知\(f(0)=2\),这意味着当\(x=0\)时,导数值为2,即\(2k=2\),解得\(k=1\)。由此,原函数变为\(f(x)=x^3+x+1\),其导数为\(f(x)=3x^2+2\)。
法线方程:y=mx+c m=一1/k; k为切线斜率 再把切点坐标代入求得c。
切线方程:对函数求导(导函数为y=2x+3),然后求出在x=1时的导数y,此时y的值为经过x=1时的切线的斜率(根据导数的几何意义),知道切线的斜率了,然后再知道一个点的坐标就可以求出。
法线方程和切线方程是数学几何学中的重要概念,切线方程的公式可以表示为y=f(a)(x-a)+f(a),其中f(a)表示在点a处的导数值,f(a)表示在点a处的函数值。法线方程则是垂直于切线的一条直线,其表达式为α*β=-1,其中α和β分别为切线和法线的斜率。
切线方程用于描述曲线在某点处的直线化,而法线方程则描述了与切线垂直的直线。在几何学中,法线是指垂直于某平面的一条虚线。对于曲线上的某点,法线是垂直于该点处切线的一条线。切线是指与曲线在某点接触的直线,且与该点处的曲线斜率相同。
根据点斜式公式,我们可以写出切线方程:y=k(x-x0)+y0=f′(x0)*(x-x0)+f(x0)。同样地,法线方程也可以表示为:y=(-1/k)(x-x0)+y0=(-1/f′(x0))*(x-x0)+f(x0)。最后,根据具体需求,可以将这些方程进一步化简为一般式或斜截式。
文章声明:以上内容(如有图片或视频亦包括在内)除非注明,否则均为网友提供,转载或复制请以超链接形式并注明出处。