三角形内切圆半径（三角形内切圆半径求法）

三角形内切圆半径、外切圆半径怎么计算?

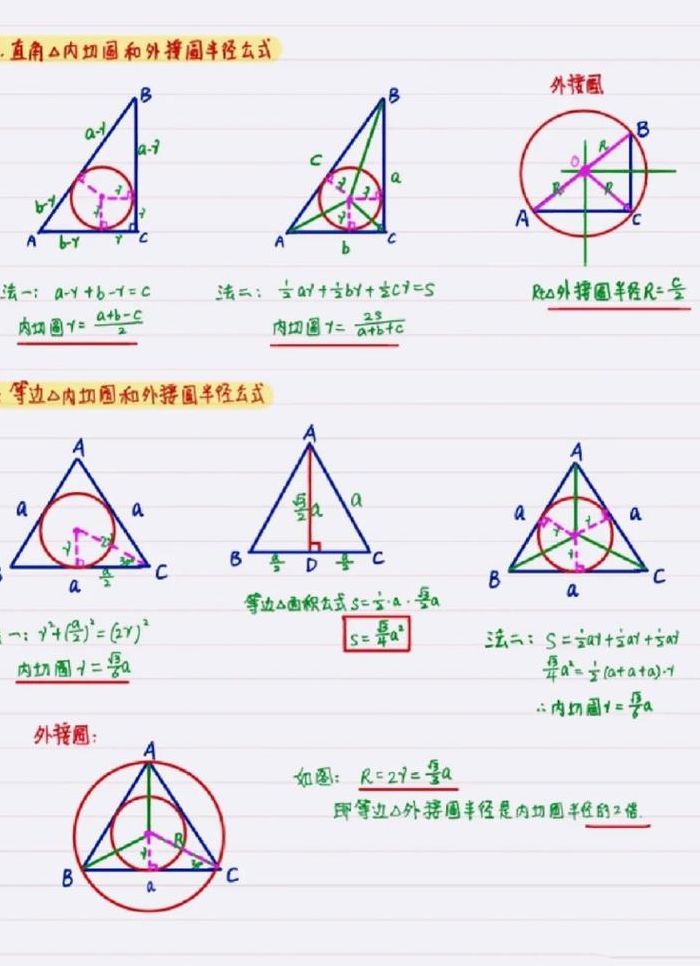
1、三角形内切圆半径：r=2s/(a+b+c)。式中s是三角形的面积，(a+b+c)是三角形的周长。三角形外接圆的半径：R=abc/4s公式中a，b，c分别为三角形的三边，S为面积。与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形。

2、三角形内切圆半径的计算公式为r=2S/(a+b+c)，外接圆半径的计算公式为R=abc/4S，其中S代表三角形面积，a、b、c为三角形三边长度。内切圆圆心位于三角形内部，是三角形三个角平分线的交点。从圆心到三角形各边的距离相等。而外接圆圆心则是任意两边垂直平分线的交点。

3、三角形内切圆半径：r=2S/（a+b+c）；三角形外接圆的半径：R=abc/4S。其中，S为三角形的面积，a，b，c分别为三角形的三边。三角形的内切圆圆心定在三角形内部，三个角的角平分线的交点是内切圆的圆心，圆心到三角形各个边的垂线段相等。

4、直角三角形的内切圆半径和外接圆半径可以利用其边长直接计算。内切圆半径的公式为r=(a+b-c)/2，其中a和b是直角三角形的两个直角边，c是斜边。外接圆半径的公式为R=C/2，C同样表示斜边的长度。为了证明内切圆半径的公式，可以利用三角形面积的计算方法。

如何求三角形内切圆的半径公式

在直角三角形的内切圆中，有这样两个简便公式：两直角边相加的和减去斜边后除以2，得数是内切圆的半径。即：r＝（a＋b－c）／2 两直角边乘积除以直角三角形周长，得数是内切圆的半径。

三角形内切圆半径：r=2s/(a+b+c)。式中s是三角形的面积，(a+b+c)是三角形的周长。三角形外接圆的半径：R=abc/4s公式中a，b，c分别为三角形的三边，S为面积。与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形。

公式： 用三角形的边和角来表示 设已知一边和它的对角，那么它的外接圆的半径R：R=a/2sinA；R=b/2sinB；R=c/2sinC；其中，A、B、C表示三角形的三个角，a、b、c分别表示三个角对应的变。

直角三角形内切圆半径为：r=（a+b-c）/2 (a，b为直角边，c为斜边)一般三角形内切圆半径为：r=2S/(a+b+c)，S是三角形的面积公式 在三角形中，三个角的角平分线的交点是内切圆的圆心，圆心到三角形各个边的垂线段相等。

三角形内切圆的半径怎么求?

R=a/2sinA；R=b/2sinB；R=c/2sinC；其中，A、B、C表示三角形的三个角，a、b、c分别表示三个角对应的变。

两直角边相加的和减去斜边后除以2，得数是内切圆的半径。即：r＝（a＋b－c）／2 两直角边乘积除以直角三角形周长，得数是内切圆的半径。

首先，根据勾股定理可知：a^2 + b^2 = c^2。内切圆与直角三角形的三边都相切，因此从内切圆心到三条边的垂直距离等于内切圆的半径r。设内切圆与直角边a、b和斜边c的切点分别为A、B和C，内切圆心为O。

三角形内切圆半径：r=2s/(a+b+c)。式中s是三角形的面积，(a+b+c)是三角形的周长。三角形外接圆的半径：R=abc/4s公式中a，b，c分别为三角形的三边，S为面积。与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形。

三角形的内切圆半径公式是怎样的?

三角形内切圆的半径公式是：r=(a+b-c)/2。与多边形各边都相切的圆叫做多边形的内切圆。特殊地，与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形。三角形的内心是三角形三条角平分线的交点。

在直角三角形的内切圆中，有这样两个简便公式：两直角边相加的和减去斜边后除以2，得数是内切圆的半径。即：r＝（a＋b－c）／2 两直角边乘积除以直角三角形周长，得数是内切圆的半径。

三角形内切圆半径：r=2s/(a+b+c)。式中s是三角形的面积，(a+b+c)是三角形的周长。三角形外接圆的半径：R=abc/4s公式中a，b，c分别为三角形的三边，S为面积。与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形。

三角形内切圆半径公式为：r = s × / ，其中r是内切圆的半径，s是三角形的半周长，n是三角形的边数。详细解释如下：三角形内切圆的概念 三角形内切圆是指与三角形的三条边都相切的圆。这个圆有一个很重要的性质，即其圆心位于三角形的内部，并且与每条边都有切点。

The End