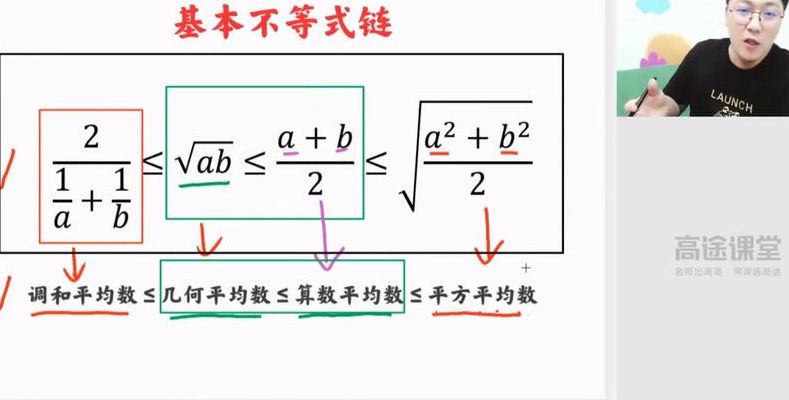
求基本不等式四个式子
1、基本不等式中常用公式(1)√((a2+b2)/2)≥(a+b)/2≥√ab≥2/(1/a+1/b)。(当且仅当a=b时,等号成立)(2)√(ab)≤(a+b)/2。(当且仅当a=b时,等号成立)(3)a2+b2≥2ab。(当且仅当a=b时,等号成立)(4)ab≤(a+b)2/4。
2、基本不等式是数学中常用的不等式关系,包括四个基本的不等式公式:算术平均-几何平均不等式、均值不等式、柯西-施瓦茨不等式和三角不等式。算术平均-几何平均不等式(AM-GM Inequality)算术平均-几何平均不等式是指对于非负实数的任意一组数,其算术平均值不小于它们的几何平均值。
3、基本不等式四个分别是a2+b2≧2ab( a,b∈R ),ab≦(a2+b2)/2(a,b∈R),a+b≧2√ab (a,b∈R﹢),ab≦[(a+b)/2]2(a,b∈R﹢)。基本不等式是主要应用于求某些函数的最值及证明的不等式。
4、基本不等式公式四个叫什么名字平方平均数、算术平均数、几何平均数、调和平均数平方平均数又名均方根(Root Mean Square),英文缩写为RMS。它是2次方的广义平均数的表达式,也可称为2次幂平均数。英文名为,一般缩写成RMS。
5、四个重要的不等式公式√((a2+b2)/2)≥(a+b)/2≥√ab≥2/(1/a+1/b);√(ab)≤(a+b)/2;a2+b2≥2ab;ab≤(a+b)2/4不等式(inequality)是用不等号连接的式子。其中四个基本的不等式公式分别叫做均方、算术平均、几何平均和调和平均。
6、基本不等式是数学中一个重要的不等式,主要用于求解某些函数的最值及证明问题。它表述为:任意两个正实数的算术平均数大于或等于它们的几何平均数。具体而言,对于任意的正数a、b,有(a+b)/2≥(a+b)/4≥ab≥(1/a+1/b)/4。
基本不等式的公式
1、四个基本不等式公式:a+b≥2ab。(当且仅当a=b时,等号成立)√(ab)≤(a+b)/2。(当且仅当a=b时,等号成立)a+b≥2√(ab)。(当且仅当a=b时,等号成立) ab≤[(a+b)/2]。(当且仅当a=b时,等号成立)。
2、基本不等式公式有:a+b≥2√(ab)。a大于0,b大于0,当且仅当a=b时,等号成立。常用不等式公式:√(a^2+b^2)/2≥(a+b)/2≥√ab≥2/(1/a+1/b);√(ab)≤(a+b)/2;a^2+b^2≥2abab≤(a+b)^2/4;||a|-|b||≤|a+b|≤|a|+|b|。
3、基本不等式公式主要是以下几个: 均值不等式:对于所有正数,其算术平均值永远大于或等于其几何平均值。公式表达为:对于任意正数a和b,有/2 。这是基于算术平均与几何平均之间的关系得出的重要不等式。平方和不等式:对于任意的实数a和b,都有 2ab。
不等式的四种基本公式是什么?
1、其中四个基本的不等式公式分别叫做均方、算术平均、几何平均和调和平均。不等式分为严格不等式与非严格不等式,用纯粹的大于号、小于号连接的不等式称为严格不等式,用不小于号(大于或等于号)、不大于号(小于或等于号)连接的不等式称为非严格不等式,或称广义不等式。
2、四个基本不等式公式如下:四个基本不等式公式:a+b≥2ab。(当且仅当a=b时,等号成立)√(ab)≤(a+b)/2。(当且仅当a=b时,等号成立)a+b≥2√(ab)。(当且仅当a=b时,等号成立) ab≤[(a+b)/2]。(当且仅当a=b时,等号成立)。
3、基本不等式公式四个叫什么名字平方平均数、算术平均数、几何平均数、调和平均数平方平均数又名均方根(Root Mean Square),英文缩写为RMS。它是2次方的广义平均数的表达式,也可称为2次幂平均数。英文名为,一般缩写成RMS。
4、基本不等式是数学中常用的不等式关系,包括四个基本的不等式公式:算术平均-几何平均不等式、均值不等式、柯西-施瓦茨不等式和三角不等式。算术平均-几何平均不等式(AM-GM Inequality)算术平均-几何平均不等式是指对于非负实数的任意一组数,其算术平均值不小于它们的几何平均值。
5、基本不等式公式有:a+b≥2√(ab)。a大于0,b大于0,当且仅当a=b时,等号成立。常用不等式公式:√(a^2+b^2)/2≥(a+b)/2≥√ab≥2/(1/a+1/b);√(ab)≤(a+b)/2;a^2+b^2≥2abab≤(a+b)^2/4;||a|-|b||≤|a+b|≤|a|+|b|。
文章声明:以上内容(如有图片或视频亦包括在内)除非注明,否则均为网友提供,转载或复制请以超链接形式并注明出处。