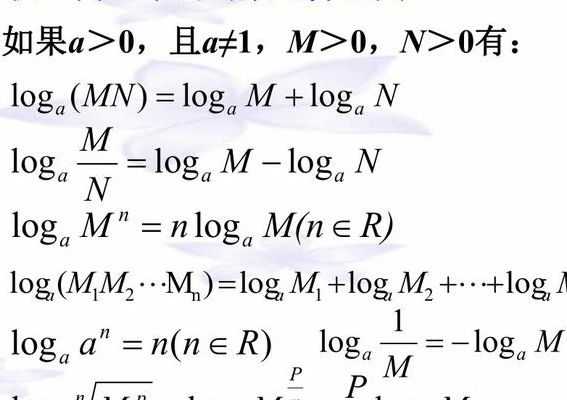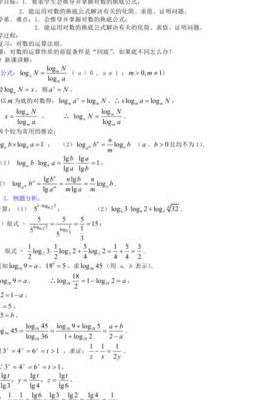对数运算法则换底公式（对数换底公式怎么来的）

log的基本运算法则?

1、log的基本运算法则如下：换底公式：loga（b）=lgam（b）/lgm（a），其中a、m、b为任意实数，且a大于0，m大于0，b大于1。log（a*b）= log（a）+ log（b），对数的加法。log（a/b）= log（a）- log（b），对数的减法。

2、log(M/N) = log(M) / log(N)换底公式导出：log(M/N) = -log(N) / log(M)对数恒等式：a^(log(M)) = M 对数函数的性质：函数 y = log(a)X，其中 a 是常数，a 0 且不等于 1，称为对数函数。它实际上是指数函数的反函数，可以表示为 x = a^y。

3、log公式运算法则有：loga(MN)=logaM+logaN；loga(M/N)=logaM-logaN；logaNn=nlogaN。运算法则loga(MN)=logaM+logaNloga(M/N)=logaM-logaNlogaNn=nlogaN(n，M，N∈R)如果a=em，则m为数a的自然对数，即lna=m，e=718281828…为自然对数的底，其为无限不循环小数。

4、对数的乘法法则：log(b， x * y) = log(b， x) + log(b， y)即，对于底数为 b 的对数函数，对于两个数的乘积，它们的对数等于各自的对数之和。

对数换底公式是什么公式?

换底公式是：log(a)(x) = log(b)(x)/log(b)(a) = lg(x)/lg(a) = ln(x)/ln(a)。在数学中，对数是乘法的逆运算，就像除法是乘法的倒数一样。对数是必须用来产生另一个固定数字（基数）的指数。在简单的情况下，对数计数乘数。

对数换底公式：log(a)(N)=log(b)(N)÷log(b)(a)。运算法则：loga(MN)=logaM+logaN。loga(M/N)=logaM-logaN。logaNn=nlogaN。(n，M，N∈R)。如果a=em，则m为数a的自然对数，即lna=m，e=718281828…为自然对数的底，其为无限不循环小数。

对数函数换底公式为：log = log / log。这是对数换底公式的直接形式。以下是 对数换底公式的推导建立在对数定义的基础上。我们知道对数函数的基本定义是：以a为底，M为真数的对数，记作logM，其定义为a的多少次方等于M。即求解a^n=M中的n值。

log运算法则公式有哪些?

1、四则运算法则 log(AB)=logA+logB；log(A/B)=logA-logB；logN^x=xlogN。换底公式 logM/N=logM/logN。换底公式导出 logM/N=-logN/M。对数恒等式 a^(logM)=M。

2、log公式运算法则有：loga(MN)=logaM+logaN；loga(M/N)=logaM-logaN；logaNn=nlogaN。运算法则loga(MN)=logaM+logaNloga(M/N)=logaM-logaNlogaNn=nlogaN(n，M，N∈R)如果a=em，则m为数a的自然对数，即lna=m，e=718281828…为自然对数的底，其为无限不循环小数。

3、log的基本运算法则如下：换底公式：loga（b）=lgam（b）/lgm（a），其中a、m、b为任意实数，且a大于0，m大于0，b大于1。log（a*b）= log（a）+ log（b），对数的加法。log（a/b）= log（a）- log（b），对数的减法。

4、对数函数是指数函数的逆运算，其基本计算公式可以表示为：\[ \log_{b}(a) = c \]这里的条件是：\[ b^c = a \]其中，\(a\) 是大于0的实数（即对数的真数），\(b\) 是大于0且不等于1的实数（即对数的底），\(c\) 是对数的结果，即\(b\) 的多少次方等于\(a\)。

对数的运算法则及公式换底

1、四则运算法则 log(AB)=logA+logB；log(A/B)=logA-logB；logN^x=xlogN。换底公式 logM/N=logM/logN。换底公式导出 logM/N=-logN/M。对数恒等式 a^(logM)=M。

2、对数的乘法法则：ln(x) + ln(y) = ln(xy)。 对数的减法法则：ln(x) - ln(y) = ln(x/y)。 对数的幂法则：ln(x^n) = nln(x)。 对数的根号法则：ln(√x) = ln(x)/2。 对数的e法则：ln(e) = 1。 对数的1法则：ln(1) = 0。

3、运算法则 loga(MN)=logaM+logaN；loga(M/N)=logaM-logaN；logaNn=nlogaN；(n，M，N∈R)；如果a=em，则m为数a的自然对数，即lna=m，e=718281828…为自然对数的底，其为无限不循环小数。定义：若an=b(a0，a≠1)则n=logab。换底公式 logMN=logaM/logaN；换底公式导出：logMN=-logNM。

4、对数的运算法则： 对数的乘法法则：log = logm + logn。 对数的除法法则：log = logm - logn。 对数的幂法则：log = n logm，其中n为实数。 对数的换底公式：logm = logp logp，其中p为真数，p0且p1。

5、对数的运算法则及公式换底如下：对数的运算法则主要包括加法法则和乘法法则。加法法则是指同底数的对数相加，等于被加数相乘后取同底数的对数，即log_a（m）+log_a（n）=log_a（mn）。乘法法则是指同底数的对数相乘，等于被乘数相乘后取同底数的对数，即log_a（m）*log_a（n）=log_a（m^n）。

6、对数的换底公式 对数换底公式是对数运算的基础，它表明以任意两个正数a和b为底数的对数之间可以通过换底公式进行转换。换底公式为：logb = lg / lg。这一公式在对数运算中非常重要，能够帮助我们将不同的对数底数统一起来，从而简化计算。

The End