减函数的定义（减函数的定义域一定要连续吗）

什么是减函数

1、减函数是指在定义域内，函数值随自变量的增大而减小，随自变量减小而增大的函数。比如：y=-x； y=1/2的x次方等。用数学语言表示就是：对于定义域为D的函数y=f(x)，若任意x1，x2满足x1，x2∈D，且x1x2，则有f(x1)＜f(x2)。

2、减函数的特点是其图像从左到右呈现下降趋势，即随着自变量x值的增加，函数值y逐渐减小。为了确定一个函数是否为减函数，可以采用定义法、观察图像法、直观判断法，或者通过分析该区间内函数导数的正负情况来进行判断。导数为负时，函数表现为递减。

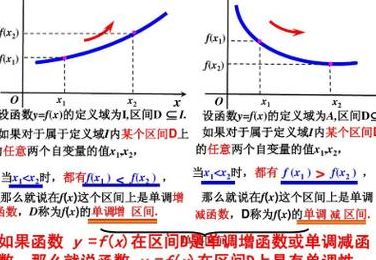
3、一般地，设函数f(x)的定义域为D，如果对于定义域D内的某个区间上的任意两个自变量的值x1，x2 ，当x1x2时，都有f(x1) f(x2)，那么就说f(x)在这个区间上是减函数。此区间叫做函数f(x)的单调减区间。随着X增大，Y减小为减函数。当x1x2时 f(x2)-f(x1)0.即为减函数。

增函数、减函数的定义

1、在数学中，增函数和减函数是描述函数变化趋势的概念。增函数（Increasing function）：如果对于在定义域上的任意两个实数x1和x2，当x1 x2时，函数值f(x1)小于f(x2)，则称函数f(x)是增函数。也就是说，随着自变量的增加，函数值也逐渐增加。

2、增函数：如果在函数的定义域内的每一个点，函数的值都比其在那个点的邻近点的函数值要大，那么我们就说这个函数是增函数。如果您在函数图上向上移动，您会看到函数的值在增加。例如，函数f(x) = x在其定义域内就是一个增函数。

3、增函数的概念是指当自变量x增大时，函数值y也随之增大。例如，函数y=x即为增函数，随x值的增加，y值也相应增加。与之相反，减函数的概念是指当自变量x增大时，函数值y也随之减小。比如，函数y=1/x即为减函数，随x值的增加，y值反而减小。

4、在函数的定义域内，如果对于任意两个数x1和x2，当x1小于x2时，f(x1)大于等于f(x2)，那么函数f(x)被称为是减函数。具体来说，对于减函数而言，随着自变量x的增加，函数值f(x)是减少的。也就是说，如果x1x2，则f(x1)≥f(x2)。需要注意的是，减函数在定义域内必须保持单调递减的特性。

5、定义：一般地，设函数f(x)的定义域为D，如果对于定义域D内的某个区间上的任意两个自变量的值x1，x2 ，当x1x2时，都有f(x1) f(x2)，那么就说f(x)在这个区间上是增函数。此区间就叫做函数f(x)的单调增区间。

6、减函数和增函数的定义基于函数值与自变量之间的关系。对于减函数而言，函数值随着自变量的增大而减小，这种性质在实际问题中非常常见。

减函数是什么

减函数是指在定义域内，函数值随自变量的增大而减小，随自变量减小而增大的函数。比如：y=-x； y=1/2的x次方等。用数学语言表示就是：对于定义域为D的函数y=f(x)，若任意x1，x2满足x1，x2∈D，且x1x2，则有f(x1)＜f(x2)。

在数学中，增函数和减函数是描述函数变化趋势的概念。增函数（Increasing function）：如果对于在定义域上的任意两个实数x1和x2，当x1 x2时，函数值f(x1)小于f(x2)，则称函数f(x)是增函数。也就是说，随着自变量的增加，函数值也逐渐增加。

定义：一般地，设函数f(x)的定义域为D，如果对于定义域D内的某个区间上的任意两个自变量的值x1，x2 ，当x1x2时，都有f(x1) f(x2)，那么就说f(x)在这个区间上是增函数。此区间就叫做函数f(x)的单调增区间。

该函数是指自变量增加时，函数值减小的函数。减函数是数学中的一个概念，指的是当自变量增加时，函数值减小的函数。换句话说，对于减函数来说，随着自变量的增加，函数值会逐渐减小。可以通过函数的导数来判断，如果函数的导数始终小于零，则说明函数是减函数。

增函数和降函数是两种描述函数增减性的术语。增函数：如果在函数的定义域内的每一个点，函数的值都比其在那个点的邻近点的函数值要大，那么我们就说这个函数是增函数。如果您在函数图上向上移动，您会看到函数的值在增加。例如，函数f(x) = x在其定义域内就是一个增函数。

减函数是指随着自变量的增加，函数值逐渐减小的函数，也被称为单调减函数，是一种常见的函数类型。相反，增函数是指随着自变量的增加，函数值逐渐增加的函数，也被称为单调增函数。这两种函数在数学分析中经常被用于研究函数的变化规律和性质。减函数和增函数之间有着密切的关系。