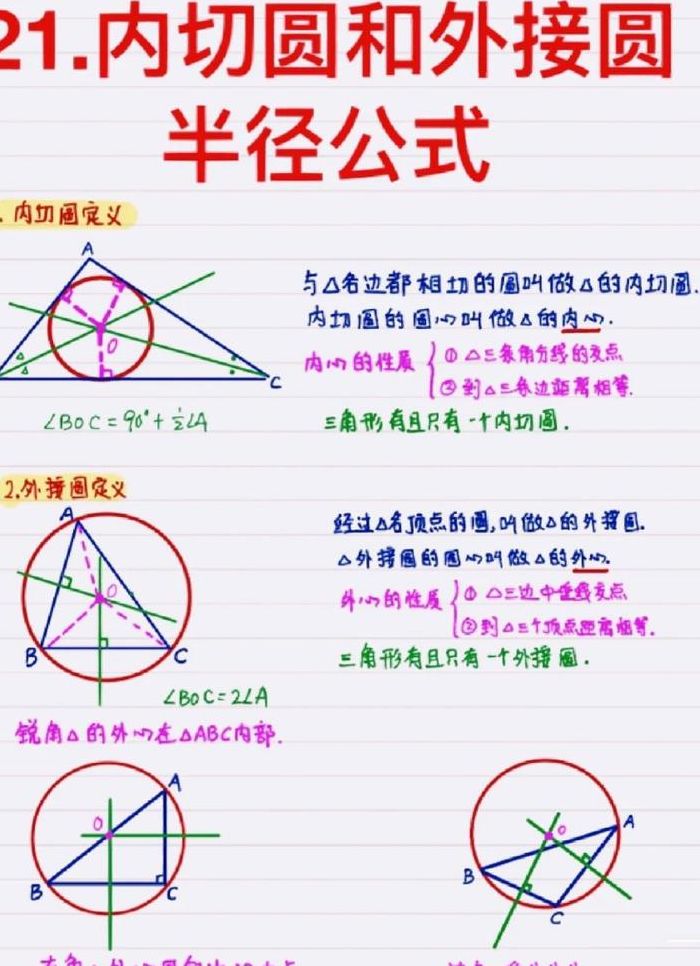
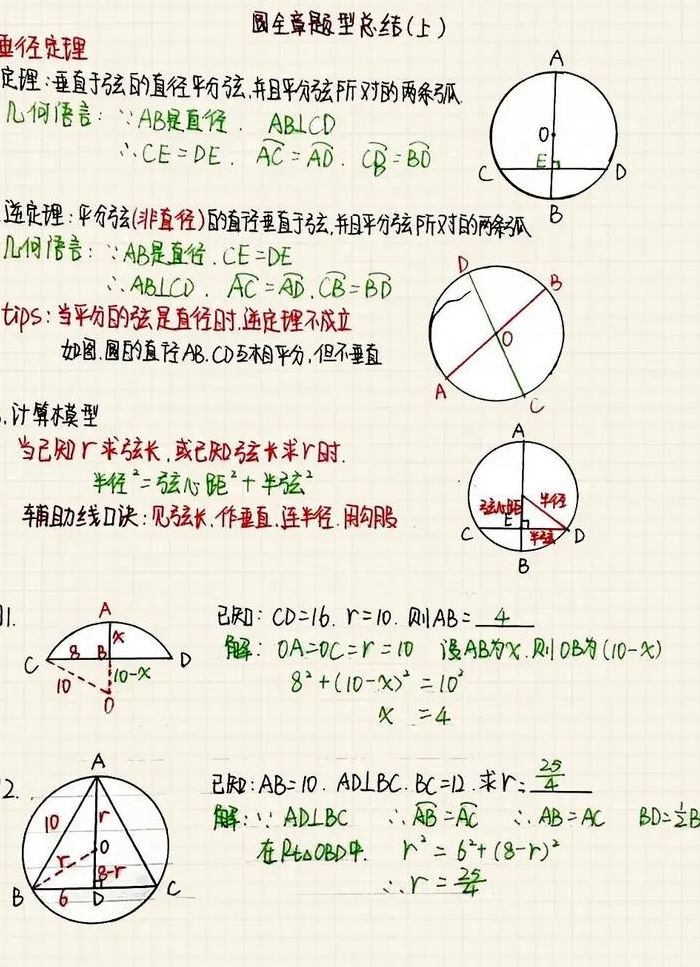
圆的半径怎么求（标准方程圆的半径怎么求）

圆的半径怎么求?

圆的一般方程是x2+y2+Dx+Ey+F=0(D2+E2-4F0)，其中圆心坐标是（-D/2，-E/2），半径 【根号（D2+E2-4F）】/2。圆是一种几何图形。根据定义，通常用圆规来画圆。 同圆内圆的直径、半径长度永远相同，圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。对称轴是直径所在的直线。

首先，我们需要知道圆的面积公式是πr，其中r是圆的半径，π是一个常数，约等于14159。然后，如果你已经知道了圆的面积A，你可以通过这个公式来求解半径r。将面积A代入公式，得到r=√（A/π）。这就是求解半径的公式。最后，你需要使用这个公式来计算半径。

已知圆的周长，求圆的直径：直径 = 周长 ÷ π（14）已知圆的周长，求圆的半径：半径 = 周长 ÷ 2 ÷ π（14）圆的方程：圆的标准方程：在平面直角坐标系中，以点O（a，b）为圆心，以r为半径的圆的标准方程是（x-a）＾2+（y-b）＾2=r^2。

所以半径R=01÷2+245×245÷(01×8)=005+460.102÷108=26183396 圆的一般方程，是数学领域的知识。圆的一般方程为x+y+Dx+Ey+F=0 (D+E-4F0)，或可以表示为(X+D/2)+(Y+E/2)=(D+E-4F)/4。

已知圆的周长，求圆的直径或半径方法如下：已知圆的周长，求圆的直径：直径 = 周长 ÷ π（14）已知圆的周长，求圆的半径：半径 = 周长 ÷ 2 ÷ π（14）依据是：圆周率。

计算圆半径：方法 1： 已知直径计算圆半径；计算公式是：D = 2r。其中“D”代表直径，“r”代表半径。公式可变换为r = D/2。方法 2： 已知周长求半径；周长公式是C= 2πr，其中“r”代表半径，π是圆周率（14.）。换算成半径公式就是r = C/2π。

圆的半径怎么算?

1、公式：圆的半径 = 周长 ÷ ，其中π约等于14。说明：如果你知道一个圆的周长，可以用这个公式来计算它的半径。通过直径计算：公式：圆的半径 = 直径 ÷ 2。说明：直径是穿过圆心、两端都在圆上的线段。如果你知道一个圆的直径，可以直接将其除以2来得到半径。

2、半径 = 周长 ÷ 2 ÷ π（14）圆的方程：圆的标准方程：在平面直角坐标系中，以点O（a，b）为圆心，以r为半径的圆的标准方程是（x-a）＾2+（y-b）＾2=r^2。圆的一般方程：把圆的标准方程展开，移项，合并同类项后，可得圆的一般方程是x^2+y^2+Dx+Ey+F=0。

3、计算圆半径：方法 1： 已知直径计算圆半径；计算公式是：D = 2r。其中“D”代表直径，“r”代表半径。公式可变换为r = D/2。方法 2： 已知周长求半径；周长公式是C= 2πr，其中“r”代表半径，π是圆周率（14.）。换算成半径公式就是r = C/2π。

4、圆的半径=周长÷2π（14），圆或圆的半径是从其中心到其周边的任何线段，并且在更现代的使用中，它也是其中任何一个的长度。这个名字来自拉丁半径，意思是射线，也是一个战车的轮辐。半径的复数可以是半径（拉丁文复数）或常规英文复数半径。半径的典型缩写和数学变量名称为r。

5、半径 = 周长 ÷ 2 ÷ π（14）依据是：圆周率。圆周率（Pi）是圆的周长与直径的比值，一般用希腊字母π（读作pài）表示，π是一个常数（约等于141592654），是代表圆周长和直径的比值。它是一个无理数，即无限不循环小数。在日常生活中，通常都用14代表圆周率去进行近似计算。

怎么求半径?

1、方法 1： 已知直径计算圆半径；计算公式是：D = 2r。其中“D”代表直径，“r”代表半径。公式可变换为r = D/2。方法 2： 已知周长求半径；周长公式是C= 2πr，其中“r”代表半径，π是圆周率（14.）。换算成半径公式就是r = C/2π。

2、求半径如下：圆心到圆上任意一点的距离都是半径r。我们可以使用勾股定理来计算圆心到圆上任意一点的距离。假设圆的圆心坐标为(x，y)，半径为r，圆上任意一点的坐标为(a，b)。根据勾股定理，可以得到方程(x-a)^2+(y-b)^2=r^2。由于我们已知圆心坐标，可以直接使用圆心坐标来计算半径。

3、半径r=L/（2π）。解答过程如下：（1）知道半圆的周长，设圆的周长为L。（2）根据圆的周长公式：L=2πr（其中r为半径），可得：半径r=L/（2π）。

4、通过圆的面积来计算出其半径。以下是具体的步骤：首先，我们需要知道圆的面积公式是πr，其中r是圆的半径，π是一个常数，约等于14159。然后，如果你已经知道了圆的面积A，你可以通过这个公式来求解半径r。将面积A代入公式，得到r=√（A/π）。这就是求解半径的公式。

圆的半径怎么求

1、已知圆的周长，求圆的直径：直径 = 周长 ÷ π（14）已知圆的周长，求圆的半径：半径 = 周长 ÷ 2 ÷ π（14）圆的方程：圆的标准方程：在平面直角坐标系中，以点O（a，b）为圆心，以r为半径的圆的标准方程是（x-a）＾2+（y-b）＾2=r^2。

2、方法 1： 已知直径计算圆半径；计算公式是：D = 2r。其中“D”代表直径，“r”代表半径。公式可变换为r = D/2。方法 2： 已知周长求半径；周长公式是C= 2πr，其中“r”代表半径，π是圆周率（14.）。换算成半径公式就是r = C/2π。

3、首先，我们需要知道圆的面积公式是πr，其中r是圆的半径，π是一个常数，约等于14159。然后，如果你已经知道了圆的面积A，你可以通过这个公式来求解半径r。将面积A代入公式，得到r=√（A/π）。这就是求解半径的公式。最后，你需要使用这个公式来计算半径。

圆的一般式的圆心和半径怎么求

1、圆的一般方程是x2+y2+Dx+Ey+F=0(D2+E2-4F0)，其中圆心坐标是（-D/2，-E/2），半径 【根号（D2+E2-4F）】/2。圆是一种几何图形。根据定义，通常用圆规来画圆。 同圆内圆的直径、半径长度永远相同，圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。对称轴是直径所在的直线。

2、圆的一般方程是x+y+Dx+Ey+F=0(D+E-4F0)，其中圆心坐标是（-D/2，-E/2），半径 【根号（D+E-4F）】/2。

3、圆一般式的圆心和半径公式介绍如下：圆的一般方程：x+y+Dx+Ey+F=0(D+E-4F0)，圆心：（-D/2，-E/2），半径：根号（D+E-4F）/2。

4、圆的一般式方程求半径和圆心如下：圆的一般方程是(x-a)^2+(y-b)^2=r^2，其中(a，b)是圆心的坐标，r是圆的半径。这个方程描述了平面上所有到圆心距离为r的点的集合。当我们在平面直角坐标系中画一个圆时，我们可以通过圆心和半径来描述它。

5、圆的标准方程：在平面直角坐标系中，以点O（a，b）为圆心，以r为半径的圆的标准方程是（x-a）＾2+（y-b）＾2=r^2。圆的一般方程：把圆的标准方程展开，移项，合并同类项后，可得圆的一般方程是x^2+y^2+Dx+Ey+F=0。和标准方程对比，其实D=-2a，E=-2b，F=a^2+b^2。

The End