计算二重积分∫∫xydxdy?
1、在空间直角坐标系中,二重积分是各部分区域上柱体体积的代数和,在xoy平面上方的取正,在xoy平面下方的取负。某些特殊的被积函数f(x,y)的所表示的曲面和D底面所为围的曲顶柱体的体积公式已知,可以用二重积分的几何意义的来计算。二重积分和定积分一样不是函数,而是一个数值。
2、(x^2-x^5)dx =(1/2)*[(x^3)/3-(x^6)/6]|[0,1] =1/12 简单来说,如果积分区域关于X轴对称,那么此时就需要看被积函数关于Y是奇函数还是偶函数,运用偶倍奇零的法则。反之亦然。需要说明的一点就是积分的对称性运用需要看两点:一个是被积函数 ,另一个是积分区域。缺一不可。
3、你计算的角度有问题,方法如下,请作参考:若有帮助,请采纳。
4、简单来说,如果积分区域关于X轴对称,那么此时就需要看被积函数关于Y是奇函数还是偶函数,运用偶倍奇零的法则。反之亦然。需要说明的一点就是积分的对称性运用需要看两点:一个是被积函数 ,另一个是积分区域。缺一不可。
5、重心等物理量。此外还可以用于概率分布函数、热力学问题以及复杂的工程问题等方面的计算。总之,xydxdy的二重积分是计算平面上函数值的一种数学方法。在进行计算时需要先确定积分区域的边界,并采用重积分的定义求解。实际应用中,二重积分可以用于处理多种不同的问题,如物理问题、工程问题、概率问题等等。
二重积分问题,这个例题3是怎么确定积分限的
又,积分区域D是由x^2+y^2=2x所围成。在直角坐标系下是第四象限,建立以原点为极点的极坐标系,则D={(ρ,θ),0≤ρ≤2cosθ,-π/2≤θ≤π/2}。∴原式=∫(-π/2,π/2)dθ∫(0,2cosθ)(4-ρ^2)ρdρ=(8/3)∫(-π/2,π/2)[1-(sinθ)^3]dθ=8π/3。
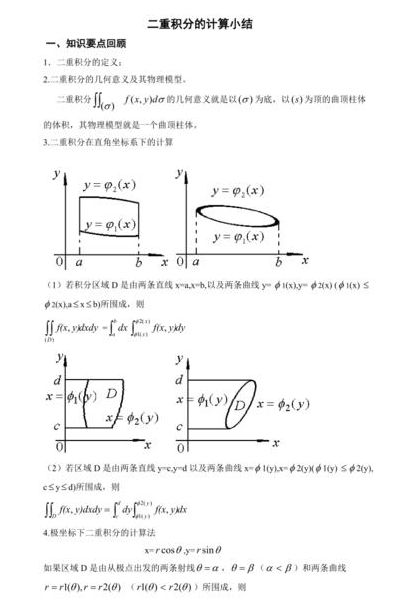
要确定二重积分的积分限,首先要绘制出封闭的积分区域。概况各类情况,无外乎是直角坐标系下和极坐标系下的区域问题。
解当把原积分化为先对y、后对x的积分时,在把x的积分限确定之后,为了确定y的积分限,通常的做法是在横轴坐标为x的变化区间内随便一点x处,作垂直于x轴的直线,从下向上看该直线时,直线进入原积分区域的点对应的纵坐标即为y的下限,直线穿出原积分区域的点对应的纵坐标为y的上限。
计算二重积分∫∫xydxdy,其中D为直线y=x与y=x^2所围成的平面区域
1、简单计算一下即可,答案如图所示 解:∫∫Dxydxdy=∫0,1xdx∫x,xydy=∫0,1x(x/2-x^4/2)dx=∫0,1(x/2-x^5/2)dx=(x^4/8-x^6/12)│0,1=1/8-1/12=1/24。
2、解:原式=∫0,2dy∫y,2yxydx =(3/2)∫0,2y^3dy =(3/2)(2^4/4)=(3/2)*4 =6:原式=∫0,1dx∫0,x^2xy^2dy =(1/3)∫0,1x^7dx =(1/3)(1^7/8)=(1/3)(1/8)=1/24。
3、y=x与y=x^2的交点为(0,0)(1,1)∫∫xydxdy =∫[0,1]∫[x^2,x]ydyxdx =∫[0,1]y^2/2[x^2,x]*xdx =∫[0,1](x^3/2-x^5/2)dx =(x^4/8-x^6/12)[0,1]=1/24。
4、y=x 与y=x交点为(0,0) (1,1)∫∫xydxdy=∫[0,1]xdx∫[x,√x]ydy =(1/2)∫[0,1](x^2-x^5)dx =(1/2)*[(x^3)/3-(x^6)/6]|[0,1] =1/12。
二重积分dxdy简单例题
二重积分$intint dxdy$的简单例题及解答如下:例题1:计算二重积分$int_{0}^{1}int_{0}^{x}dydx$。解首先,我们识别出这是一个先对$y$后对$x$进行积分的二重积分。对于内层积分$int_{0}^{x}dy$,由于被积函数为1(常数),所以积分结果为$y$在$[0,x]$上的增量,即$x-0=x$。
简单计算一下即可,答案如图所示楼上错的,楼上当作矩形区域算了首先本题区域关于x轴对称,y关于y是一个奇函数,因此积分为0,所以被积函数中的y可去掉。
这个是最简单的二重积分,因为x,y相互取值上是独立的(没有影响)。因此只需要分别对x,y积分就行了。比如先积x,就是(x+y)dx的积分在(0,1)上的值,把y看成常数。
具体回答如图:重积分有着广泛的应用,可以用来计算曲面的面积,平面薄片重心等。平面区域的二重积分可以推广为在高维空间中的(有向)曲面上进行积分,称为曲面积分。
换成极坐标,ρ=x+y≤4,ρ≤2,dxdy是微面积,换成dS符号。
双重积分怎么计算的,有例题,希望能解释一下算法谢谢(如图中的题)
把二重积分化成二次积分,也就是把其中一个变量当成常量比如Y,然后只对一个变量积分,得到一个只含Y的被积函数,再对Y积分就行了。
积分(从0到2pi)da 积分(从1到R)r(cosa+sina)/r^4*rdr=0 或直接利用对称性知道积分值是0。令R趋于无穷知道极限是0。
解:两种算法结果是一样的!如果不一样,那就是算错了!用直角坐标时,最后要用变量替换才 能求出最后结果,替换后就会出来π。
文章声明:以上内容(如有图片或视频亦包括在内)除非注明,否则均为网友提供,转载或复制请以超链接形式并注明出处。