初等函数的定义（一元初等函数的定义）

什么是初等函数(什么是初等函数和非初等函数)

初等函数是由幂函数、指数函数、对数函数、三角函数、反三角函数与常数经过有限次的有理运算及有限次函数复合所产生，并且能用一个解析式表示的函数。非初等函数是指凡不是初等函数的函数。

初等函数，顾名思义，是由幂函数、指数函数、对数函数、三角函数和反三角函数，再加上常数，通过有限次的有理运算（包括加、减、乘、除、有理数次的乘方和开方）以及有限次的函数复合所构成的函数。这些运算确保了初等函数可以用单一的解析表达式来完整描述。

非初等函数的具体特点如下： 定义：非初等函数是指不属于初等函数范畴的函数。 举例：大部分分段函数以及特殊函数都是非初等函数。但需要注意的是，也有个别分段函数是初等函数。 发展与应用：非初等函数的研究与发展是近现代数学的重大成就之一，它们在概率论、物理学等多个领域有十分广泛的应用。

初等函数是指由幂函数、常数函数、对数函数、指数函数、三角函数和反三角函数(统称基本初等函数)通过有限次加减乘除、乘开方、有限次复合等运算，且能以一个表达式表示的函数(无论是显函数还是隐函数)。不符合上述定义形式的函数，称之为非初等函数。

初等函数的基本定义是基本初等函数经过有限次的四则运算或有限次的函数复合所构成并可以用一个解析式表出的函数，称为初等函数。包括代数函数和超越函数。基本初等函数是实变量或复变量的指数函数、对数函数、幂函数、三角函数和反三角函数经过有限次四则运算及有限次复合后所构成的函数类。

初等函数：在微分域中，初等函数对应的微分扩张是初等扩张，即它们遵循特定的微分代数结构规则。非初等函数：其微分扩张则不满足这些特定的结构规则，因此无法归类为初等函数。Liouville定理的应用：该定理提供了一个判断函数是否为初等函数的工具。

y=√(sinx-3)是初等函数吗?

1、正割函数 y =sec(x)余割函数 y =csc(x)（6）反三角函数：反正弦函数 y =arcsinx 反余弦函数 y =arccosx 反正切函数 y =arctanx 反余切函数 y =arccotx （反正割函数、反余割函数一般不用）所谓初等函数就是由基本初等函数经过有限次的四则运算和复合而成的函数。

2、y=3sinx是常数函数与正弦函数乘积得到的。y1=3，y2=sinx，这两个函数是基本初等函数。y=3sinx是初等函数。其图像是由y=sinx的纵坐标伸长为原来的3倍得到的。

3、= sinx=√(1-t)，你漏了个根号！即使有根号，这个积分(-2)∫dt/√(1-t)的原函数依然无法用初等函数表示，需用第一类椭圆积分。

4、y=arcsinx为y=sinx的反三角函数，函数的定义域为函数y=sinx的值域。所以y=arcsinx定义域为［-1，1］-1≤x-3≤1，2≤x≤4，y=arcsin(x-3)定义域为［2，4］。求函数定义域的方法：函数f(x+1)的定义域为(0，1)，指的是x取值在0，1之间，那么x+1取值为1，2之间。

5、y=sin2x是初等函数，但不是基本初等函数。 y=sinx是基本初等函数。

什么是初等函数和非初等函数

1、初等函数是由幂函数、指数函数、对数函数、三角函数、反三角函数与常数经过有限次的有理运算及有限次函数复合所产生，并且能用一个解析式表示的函数。非初等函数是指凡不是初等函数的函数。

2、初等函数，顾名思义，是由幂函数、指数函数、对数函数、三角函数和反三角函数，再加上常数，通过有限次的有理运算（包括加、减、乘、除、有理数次的乘方和开方）以及有限次的函数复合所构成的函数。这些运算确保了初等函数可以用单一的解析表达式来完整描述。

3、非初等函数的具体特点如下： 定义：非初等函数是指不属于初等函数范畴的函数。 举例：大部分分段函数以及特殊函数都是非初等函数。但需要注意的是，也有个别分段函数是初等函数。 发展与应用：非初等函数的研究与发展是近现代数学的重大成就之一，它们在概率论、物理学等多个领域有十分广泛的应用。

4、初等函数是指由幂函数、常数函数、对数函数、指数函数、三角函数和反三角函数(统称基本初等函数)通过有限次加减乘除、乘开方、有限次复合等运算，且能以一个表达式表示的函数(无论是显函数还是隐函数)。不符合上述定义形式的函数，称之为非初等函数。

5、初等函数的基本定义是基本初等函数经过有限次的四则运算或有限次的函数复合所构成并可以用一个解析式表出的函数，称为初等函数。包括代数函数和超越函数。基本初等函数是实变量或复变量的指数函数、对数函数、幂函数、三角函数和反三角函数经过有限次四则运算及有限次复合后所构成的函数类。

6、初等函数：是复有理函数域的扩张中尤为基础的元素，这些函数可以通过有限次的代数、对数或指数扩张来构建。非初等函数：则无法通过上述有限次扩张来构建，其微分扩张不具备初等函数所特有的结构特征。

初等函数有哪些?

1、初等函数指一次函数，二次函数等幂函数，正弦函数，余弦函数，正切函数等三角函数，正比例函数，反比例函数，指数函数，对数函数，以上都是基本初等函数。这些函数的组合都是初等函数。如果是n（n=2)个基本初等函数复合而成的函数，则是复合函数。一般地，初等函数也包括复合函数。

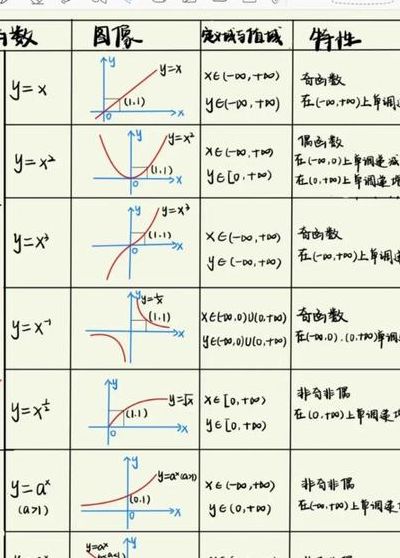
2、基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数以及它们的反函数。常数函数：是最简单的函数之一，无论自变量如何变化，其函数值始终为一个常数，形式上表示为y = c。幂函数：自变量与因变量之间具有幂次关系的函数，形式为y = x^n，其中n的正负及大小决定了函数的增减性和图形。

3、初等函数是一种可以使用有限次的有理运算和有限次函数复合来定义的函数。具体来说，这类函数可以由幂函数、指数函数、对数函数、三角函数、反三角函数与常数通过加、减、乘、除、有理数次乘方、有理数次开方等基本运算组合而成，且能通过一个解析式来表示。例如，常函数y=2就是一个简单的初等函数。

4、基本初等函数主要包括五类：幂函数、指数函数、对数函数、三角函数以及反三角函数。幂函数的形式为f(x) = xα，其中α是常数，可以是自然数、有理数，甚至可以是任意实数或复数。指数函数则指形如f(x) = ax的函数，其中a 0且a ≠ 1。

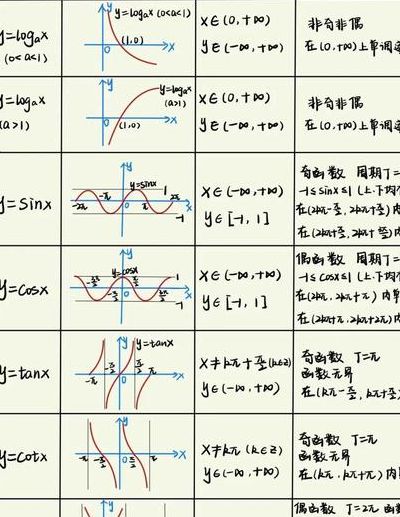
5、基本初等函数主要包括五类：常数函数 y = c，幂函数 y = x^a（a 为常数），指数函数 y = a^x（a 0， a ≠ 1），对数函数 y = log(a)x（a 0， a ≠ 1， x 0），以及三角函数和它们的反函数，如正弦函数 y = sinx 和反正弦函数 y = arcsin x 等。

初等函数和基本初等函数

1、初等函数与基本初等函数的概念存在显著差异，初等函数的范围更广，它包含了基本初等函数。基本初等函数可以看作是基础单元，分为幂函数、指数函数、对数函数、三角函数及反三角函数五种类型，这些都是单独存在的简单函数。

2、不一样，初等函数指一次函数，二次函数等幂函数，正弦函数，余弦函数，正切函数等三角函数，正比例函数，反比例函数，指数函数，对数函数，以上都是基本初等函数。而这些函数的组合都是初等函数。而复合函数是函数与函数的复合，可以是初等函数，但不只是初等函数，还有其他的很多函数。

3、基本初等函数主要分为六类：常数函数y=c（c为常数），指数函数y=a^x（a0，且a≠1），对数函数y=log(a，x)（a0且a≠1，这里的a是底数，x是自变量），幂函数y=x^a（a为实数），三角函数y=sin(x)，y=cos(x)，y=tan(x)和反三角函数y=arcsin(x)，y=arccos(x)，y=arctan(x)。

4、初等函数和基本初等函数的范围不同，初等函数包括基本初等函数。实际上初等函数是由基本初等函数经过有限次的四则运算和复合运算所得到的函数。基本初等函数有幂函数、指数函数、对数函数、三角函数、反三角函数这五类，就是简单的单独的一个函数。

5、这两个函数区别有包含范围不同、表示方法不同。包含范围不同：基本初等函数是初等函数的基础组成部分，初等函数包含基本初等函数。表示方法不同：基本初等函数只能用基本的代数和三角运算表示，初等函数除了可以用初等解析式表示以外，往往还有其他表示形式。

初等函数的定义是什么

初等函数是一种可以使用有限次的有理运算和有限次函数复合来定义的函数。具体来说，这类函数可以由幂函数、指数函数、对数函数、三角函数、反三角函数与常数通过加、减、乘、除、有理数次乘方、有理数次开方等基本运算组合而成，且能通过一个解析式来表示。例如，常函数y=2就是一个简单的初等函数。

初等函数，作为一种广泛应用于数学、物理乃至工程领域的基础函数类型，是由基本初等函数通过有限次的四则运算或函数复合构成的函数。这些基本初等函数包括幂函数、指数函数、对数函数、三角函数、反三角函数，以及由这些函数构成的双曲函数，如双曲正弦、双曲余弦、双曲正切、双曲余切、双曲正割、双曲余割。

初等函数定义：由常数和基本初等函数经过有限次四则运算和有限次函数复合步骤所构成并可用一个式子表示的函数。

The End