单纯形法计算步骤（单纯形法计算步骤思维导图）

单纯形法的计算步骤

1、单纯形法是一种求解线性规划问题的迭代算法，其基本计算步骤包括： 构造初始可行解。 检查当前解是否是最优解。 若不是最优解，则根据一定的规则选择离开变量和进入变量。 更新当前解，并重复步骤2，直到找到最优解。首先，需要构造一个初始可行解。

2、第一步：基于约束条件方程组的系数矩阵，通过寻找或构造单位矩阵的方法，确定基变量，从而求出初始基本可行解，再利用初始基本可行解及线性规划模型提供的信息，编制初始单纯形表。

3、关于这个问题，单纯形法的计算步骤如下： 将标准型线性规划问题表示成矩阵形式。 根据标准型线性规划问题的矩阵形式构造初始可行解。 计算初始可行解的目标函数值，如果是最小化问题，则将目标函数系数取相反数。 如果初始可行解是最优解，则直接输出结果。

4、在开始单纯形法计算之前，首先需要基于约束条件方程组的系数矩阵，通过寻找或构造单位矩阵的方法，来确定基变量，从而求出初始基本可行解。这个步骤中，我们需要利用初始基本可行解及线性规划模型提供的信息，编制初始单纯形表。这个初始单纯形表将成为我们后续计算的基础。

单纯形法计算步骤详解

在开始单纯形法计算之前，首先需要基于约束条件方程组的系数矩阵，通过寻找或构造单位矩阵的方法，来确定基变量，从而求出初始基本可行解。这个步骤中，我们需要利用初始基本可行解及线性规划模型提供的信息，编制初始单纯形表。这个初始单纯形表将成为我们后续计算的基础。

单纯形法是求解线性规划问题最常用、最有效的算法之一。它的计算步骤如下：把线性规划问题的约束方程组表达成典范型方程组，找出基本可行解作为初始基本可行解 。若基本可行解不存在，即约束条件有矛盾，则问题无解。

第一步：基于约束条件方程组的系数矩阵，通过寻找或构造单位矩阵的方法，确定基变量，从而求出初始基本可行解，再利用初始基本可行解及线性规划模型提供的信息，编制初始单纯形表。

单纯形法具体有哪两种方法?

单纯形法是一种求解线性规划问题的通用方法，由美国数学家G.B.丹齐克于1947年提出。其理论基础在于：线性规划问题的可行域为n维向量空间Rn中的多面凸集，其最优解若存在，则必在该凸集的某个顶点处取得。顶点对应的可行解称为基本可行解。

对偶单纯形法 1954年美国数学家C.莱姆基提出对偶单纯形法。单纯形法是从原始问题的一个可行解通过迭代转到另一个可行解，直到检验数满足最优性条件为止。对偶单纯形法则是从满足对偶可行性条件出发通过迭代逐步搜索原始问题的最优解。在迭代过程中始终保持基解的对偶可行性，而使不可行性逐步消失。

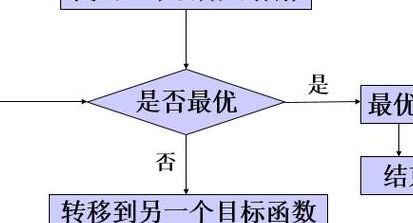
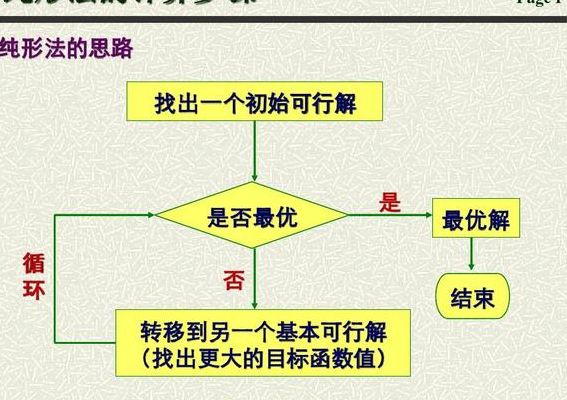
单纯形法基本思想 先找一个基可行解（顶点），判断是否为最优解。如果是，那么找到啦，结束。如果不是，则沿着可行域的边缘移动，保证这条边缘的移动方向 让目标函数值不断增大，直至挪到另一个顶点；判断该顶点是否最优解，不是则继续移动，直到找到最优解为止。

单纯形法和对偶单纯形法是用于求解线性规划问题的两种常用方法。它们的原理分别是通过迭代寻找可行解和最优解，但具体操作和对问题的理解有所不同。对偶单纯形法可以看作是单纯形法的一种拓展，用于处理某些特殊情况下的问题。单纯形法是一种通过迭代寻找线性规划问题最优解的方法。

单纯形法检验数怎么算

用基变量在目标函数中的系数，乘以你要算得那个变量对应的系数列的各个值，并求和，再减去要算得那个变量在目标函数中对应的系数，就是检验数。

在目标函数中用非基变量代替基变量，所得系数即是检验数。在目标规划中，p1p2p3不是具体算出来的值，而是按照原先的方法在草纸上写出计算校验数的式子，系数有p1p2p3就带着，整理会得到一个关于p1p2p3的式子，那一列填的就是这个式子中p1p2p3的系数，就这样一列一列就可以填好。

在单纯形法中，检验数的计算是至关重要的步骤。具体计算方法是：首先，将基变量在目标函数中的系数与要计算的变量对应的系数列的各个值相乘，并对这些乘积求和。然后，从上述和中减去要计算的变量在目标函数中对应的系数，即可得到该变量的检验数。

The End