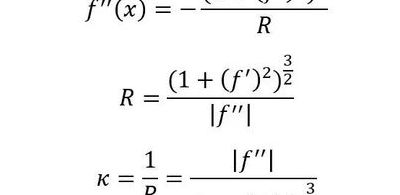曲率中心坐标（曲率中心坐标的计算公式推导）

通过坐标点计算曲率

1、没有函数咋求导啊！正解如下：由已知坐标拟合出函数近似曲线。选择什么样的拟合函数，要把坐标大致画出来，人为观察根据经验看看近似什么类型的函数，然后设定合适的拟合函数，用matlab拟合出坐标的近似函数。

2、通过计算曲线的导数和二阶导数，可以求得曲率最大的点。要求曲率最大的点，首先需要计算曲线的导数和二阶导数。对于给定曲线的三维坐标函数r（t），可以求得曲线的首导数向量dr/dt和二阶导数向量d2r/dt2。

3、写出曲率圆的直角坐标方程 根据导数的计算结果，可以确定曲率圆心在切线和法线方向上的坐标，以及曲率圆的半径。曲率圆的半径等于曲线在该点的曲率值。

4、在空间曲线的情况下，曲率半径是曲率向量的长度。在平面曲线的情况下，则R要取绝对值。其中s是曲线上固定点的弧长，α是切向角，K是曲率。

5、绘制函数图像时，了解每个点的斜率有助于描绘出准确的图像形状。通过计算斜率，可以确定曲线在不同点的趋势和曲率。 物理学中的速度和加速度 在物理学中，速度和加速度与位置-时间图像之间的斜率有密切关系。

曲率圆方程怎么求

1、= ((1 + y^2)^3) / (y^2)= r = (1 + y^2)^(3/2)/ y曲率就是1/r；有了半径r、法线斜率(-1/y)，就很容易的求出曲率圆的圆心了，继而求出曲率圆的方程。不知道对你有帮助没有。

2、曲率是描述曲线弯曲程度的一个物理量，是在某一点上曲线的弯曲程度的倒数，也可以理解为曲线在该点上的圆弧半径。

3、曲率圆方程是描述曲线在某一点处的弯曲程度的数学工具，它是由曲线在该点的切线和法线构成的。在微积分中，我们经常需要找到原函数，也就是一个函数的不定积分。

4、对曲率圆方程求导， 得y的一阶导， 最后代入M点的数据，得出结果。最重要的是曲率的定义。其次是曲率圆、曲率中心、曲率半径的定义、曲率和曲率半径的关系。最后是曲率的求法（求曲率的公式）。

曲率中心ab的坐标为这个怎么来的。

1、另外两个设为AB）那么AB的中点D与AC中点的连线便是中位线，AB的中点与BC中点连线也是中位线。由于平行和二分之一的关系，坐标便是横坐标之和的平均数，纵坐标的平均数。不懂可以追问。

2、之前有考过，1995考研数学二考过一个8分的大题，低推导曲率中心坐标的，只要大纲上有就有可能考，那么简单的一个公式记一下也不费时间，万一考了，自己做过准备也不用担心。

3、曲率中心坐标公式考研可能会考，近十年没有考过，但在1995考研数学二考过一个8分的大题，低推导曲率中心坐标的。只要大纲上有就有可能考，那么简单的一个公式记一下也不费时间，万一考了，自己做过准备也不用担心。

如何确定一个椭圆的曲率中心?

椭圆准线位置在L=±a/c处，c为焦点横坐标，a为右顶点横坐标。在平面直角坐标系中，用方程描述了椭圆，椭圆的标准方程中的“标准”指的是中心在原点，对称轴为坐标轴。

椭圆的曲率计算方法如下：在微分几何中，曲率的倒数就是曲率半径，即R=1/K。平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。

过椭圆上一点作椭圆的切线，然后作这条切线的垂线，并且使得这条垂线也与椭圆相切，那么得到一个垂足为A，类似地，再任意获得两个垂足B和C，那么ABC的外接圆圆心就是椭圆的中心，而这个外接圆称为椭圆的伴随圆。

椭圆的焦点可以通过以下步骤确定：给定椭圆的长轴长度（2a）和短轴长度（2b），其中 a b。确定椭圆的中心点（h，k）。使用椭圆的定义特性，根据方程 (x-h)^2/a^2 + (y-k)^2/b^2 = 1 来确定焦点的位置。

一道高数题求解这道题

1、∴y= 不符合题意，舍去。∴点P的坐标为(2，﹣ )。②若OB=PB，则42+|y+ |2=42，解得y=﹣ 。∴点P的坐标为(2，﹣ )。③若OP=BP，则22+|y|2=42+|y+ |2，解得y=﹣ 。∴点P的坐标为(2，﹣ )。

2、解答过程如下：该题要求f（x，y）分别对x和对y的偏导等于0，并求出满足条件的x和y值。该题首先要求出f（x，y）对x和对y的偏导。并令其等于0。联立得到的两个方程组。如图所示。然后解方程即可得解。

3、分享解法如下。(1)，由题设条件，有f(x)=a(x-4x+3)。∴f(x)=∫f(x)dx=a(x/3-2x+3x)+C。又，f(1)=6，f(3)=2。∴f(1)=a(4/3)+C=6，f(3)=C=2。∴a=3。

双曲线两个图像的顶点坐标分别是什么?

1、双曲线和它的对称轴有两个交点，它们叫做双曲线的顶点。

2、双曲线顶点坐标公式：y=a(x-h)+k。一般的，双曲线（希腊语“περβολ”，字面意思是“超过”或“超出”）是定义为平面交截直角圆锥面的两半的一类圆锥曲线。

3、双曲线的图像通常有两个分支，每个分支都有一个顶点。

The End