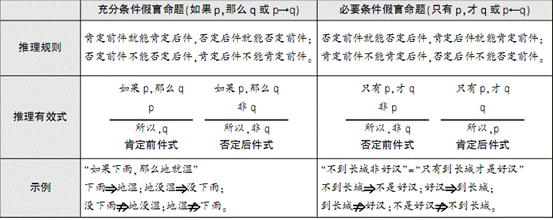
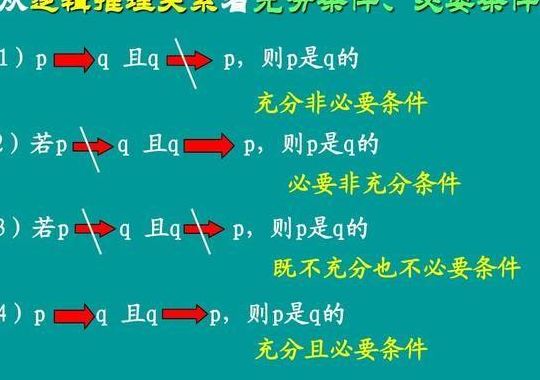
充分条件,必要条件,充要条件的定义
必要条件:如果没有A,则必然没有B;如果有A而未必有B,则A就是B的必要条件,记作B→A,读作“B蕴涵于A”。数学上简单来说就是如果由结果B能推导出条件A,我们就说A是B的必要条件。
必要条件是数学中的一种关系形式。如果没有A,则必然没有B;如果有A而未必有B,则A就是B的必要条件,记作B→A,读作“B含于A”。数学上简单来说就是如果由结果B能推导出条件A,我们就说A是B的必要条件。
定义:一般地,如果b成立,那么a成立,即b=a,或者,如果a不成立,那么b就不成立,这时,条件a就是b的必要条件。
范围不同:充要条件”包含了“充分条件”和“必要条件”,范围比两者都要更大,而“充分条件”和“必要条件”则包含了小部分条件不是完整的。
什么是充分必要条件?
充分条件:有甲这个条件—定会推出乙这个结果,有乙这个结果不一定是甲这唯一个条件。必要条件:有甲这个条件不一定能推出乙这个结果,但乙这个结果一定要有甲这个条件。
必要条件:如果能由结论推出条件,但由条件推不出结论,此条件为必要条件。
充分条件和必要条件是逻辑和数学中的两个重要概念,用于描述事件或条件之间的关系。它们有助于我们理解何时某个条件是发生或成立的充分条件,以及何时某个条件是发生或成立的必要条件。
充分必要条件,是数学学科的一个知识点。定义:如果有事物情况A,则必然有事物情况B;如果没有事物情况A,则必然没有事物情况B,A就是B的充分必要条件。
充分必要条件也即充要条件,意思是说,如果能从命题p推出命题q,而且也能从命题q推出命题p ,则称p是q的充分必要条件,且q也是p的充分必要条件。
充分条件:由条件a推出条件b,但是条件b并不一定能推出条件a。天下雨了,地面一定湿,但是地面湿不一定是下雨造成的。必要条件:由后一个条件推出前一个条件,但是前一个条件并一定能推出后一个条件。
充分必要条件是什么?
充分必要条件是一个逻辑概念,用于描述一个命题或一个陈述的特定性质。它表示某个条件是实现某个结果所必需的,并且没有其他条件可以替代它。换句话说,这个条件既是必要条件,也是充分条件。
充分条件表明条件的满足足以导致事件或结论的发生。必要条件表示某个事件或结论发生的前提条件。在逻辑推理和数学证明中,了解充分条件和必要条件的概念非常重要,因为它们有助于确定逻辑关系并构建有效的论证。
必要条件:如果能由结论推出条件,但由条件推不出结论,此条件为必要条件。
文章声明:以上内容(如有图片或视频亦包括在内)除非注明,否则均为网友提供,转载或复制请以超链接形式并注明出处。