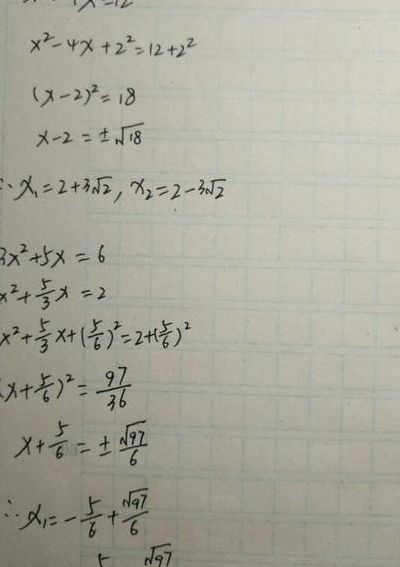配方法的步骤例题（配方法的步骤例题及答案）

二次函数配方法关于二次函数配方法

确定a、b和c的值，其中a不等于零。这些值是二次函数的系数，分别代表二次项、一次项和常数项。 计算出二次项的平方项，也就是(a/2) = (a/4)。

二次函数配方法的步骤：将二次函数的一般式化为完全平方的形式，即ax+bx+c=a（x+b/2a）+（4ac-b）/4a。确定二次函数的对称轴，即x=-b/2a。

首先，将二次函数表达式化为一般式，确定二次项系数a，一次项系数b，常数项c。其次，将二次项系数a除以2，即a/2。然后，令x等于-b除以2a，求出顶点横坐标，将顶点横坐标代入表达式，求出顶点纵坐标。

二次函数配方的步骤如下：将二次函数的一般形式写成完成平方的形式，即将二次项和常数项分开。例如，f（x）=ax^2+bx+c可以写为f（x）=a（x^2+（b/a）x）+c。

数学配方法和十字交叉法

x2=1 二次函数配方法技巧：y=ax^2-bx+c 转换为 y=a(x+h)^2+k =a(x+b/2a)^2+(c-b^2/4a)【十字相乘法】十字相乘法能把某些二次三项式分解因式。

通过二元一次方程的解法，我们可以得到X = 8 + 1/3，Y = 4/3。十字交叉法的应用现在，我们使用十字交叉法来解决一个百分比问题。已知两个百分比：30% 和 75%。我们还知道它们的用量比为25%：20%=5：4。总的量为8KG。

十字交叉法是一种数学方法，用于解决两个变量之间的比例问题。在浓度问题中，十字交叉法用于确定两种不同浓度的溶液混合后的浓度。具体来说，假设有两种不同浓度的溶液A和B，它们的浓度分别为a和b。

十字交叉法介绍 十字交叉法最初用于解决溶液混合问题，求解混合前或者混合后的溶液质量或浓度。

二次函数怎么配方法?

二次函数简单的配方法：把二次项系数提出来。在括号内，加上一次项系数一半的平方，同时减去，以保证值不变。这时就能找到完全平方了。然后再把二次项系数乘进来即可。

二次函数一般式化为顶点式的公式是：y=ax+bx+c，化为顶点式的公式是：y=a(x+b/2a)+(4ac-b)/4a。

二次函数配方法的步骤：将二次函数的一般式化为完全平方的形式，即ax+bx+c=a（x+b/2a）+（4ac-b）/4a。确定二次函数的对称轴，即x=-b/2a。

配方公式二次函数如下：首先，明确的是配方法就是将关于两个数(或代数式，但这两个一定是平方式)，写成（a+b）^2的形式或（a-b）^2的形式。将（a+b）^2的展开，得（a+b)^2=a^2+2ab+b^2。

配方法求值域的例题及解析

配方法 解题步骤：第一步 将二次函数配方成y=a(xb)2+c；第二步 根据二次函数的图像和性质即可求出函数的值域.注意点：要注意函数的定义域，有时候出题人为了迷惑学生，会特意让完全平方式的零点不在定义域内。

求值域的方法有哪些如下：观察法 通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。例1求函数y=3+√(2-3x)的值域点拨：根据算术平方根的性质，先求出√(2-3x)的值域。

一．观察法通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。例1求函数y=3+√(2－3x)　的值域。点拨：根据算术平方根的性质，先求出√(2－3x)　的值域。

直接法：从自变量的范围出发，推出值域。观察法：对于一些比较简单的函数，可以根据定义域与对应关系，直接得到函数的值域。配方法：（或者说是最值法）求出最大值还有最小值，那么值域就出来了。

．观察法 通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。用于简单的解析式。

练习：求函数y=(10x+10-x)/(10x-10-x)的值域。(答案：函数的值域为{y∣y1}) 配方法 当所给函数是二次函数或可化为二次函数的复合函数时，可以利用配方法求函数值域 例3：求函数y=√(-x2+x+2)的值域。

The End