两直线平行斜率的关系（两直线平行斜率的关系坐标）

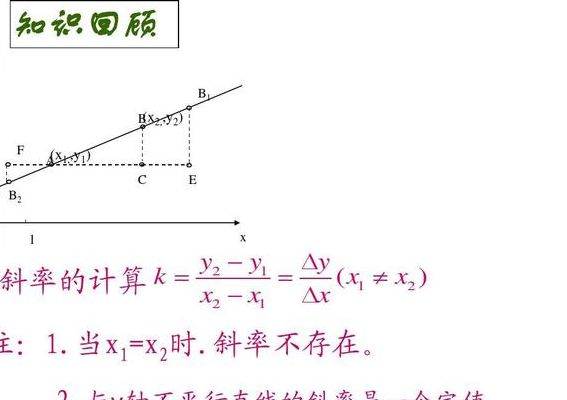
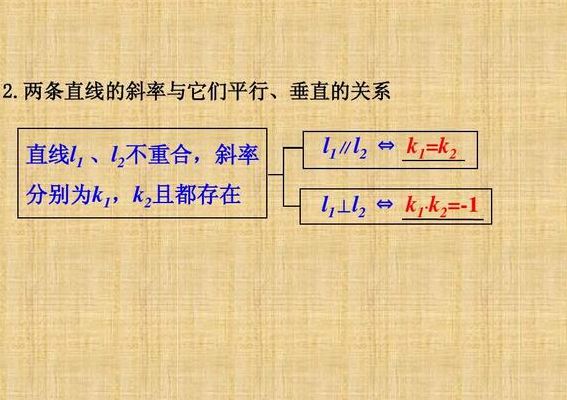
两条直线平行的斜率有什么关系

两直线平行，它们的斜率相等。斜率，亦称“角系数”，表示一条直线相对于横轴的倾斜程度。一条直线与某平面直角坐标系横轴正半轴方向的夹角的正切值即该直线相对于该坐标系的斜率。

它们的斜率相同。因为两条平行直线的斜率必须相等，才能保证它们在平面上不会相交。换句话说，如果两条直线的斜率不相等，那么它们一定不平行。因此，我们可以通过比较两条直线的斜率来确定它们是否平行。

它们在坐标系中会平行且距离相等。由于直线的斜率可以表示为直线上的任意两点的坐标之差的比值，因此，两条平行直线的斜率相等。例如，对于两条直线y=mx+b1和y=mx+b2，它们的斜率都为m，因此它们是平行的。

两直线平行，斜率相等。两直线垂直，斜率互为负倒数。所以两直线平行，斜率相乘为原来斜率的平方。两直线垂直，斜率相乘为-1。斜率又称“角系数”，是一条直线对于横坐标轴正向夹角的正切，反映直线对水平面的倾斜度。

两条直线平行与斜率之间的关系

两直线平行，它们的斜率相等。斜率，亦称“角系数”，表示一条直线相对于横轴的倾斜程度。一条直线与某平面直角坐标系横轴正半轴方向的夹角的正切值即该直线相对于该坐标系的斜率。

两直线平行，斜率相等。斜率是表示一条直线（或曲线的切线）关于（横）坐标轴倾斜程度的量。它通常用直线（或曲线的切线）与（横）坐标轴夹角的正切，或两点的纵坐标之差与横坐标之差的比来表示。两直线平行，斜率相等。

它们的斜率相同。因为两条平行直线的斜率必须相等，才能保证它们在平面上不会相交。换句话说，如果两条直线的斜率不相等，那么它们一定不平行。因此，我们可以通过比较两条直线的斜率来确定它们是否平行。

两直线平行斜率的关系

两直线平行，它们的斜率相等。斜率，亦称“角系数”，表示一条直线相对于横轴的倾斜程度。一条直线与某平面直角坐标系横轴正半轴方向的夹角的正切值即该直线相对于该坐标系的斜率。

平行直线具有相同的斜率。平行直线是位于同一平面中的两条不相交且方向相同的直线，它们在坐标系中会平行且距离相等。由于直线的斜率可以表示为直线上的任意两点的坐标之差的比值，因此，两条平行直线的斜率相等。

两条直线的斜率相等是两条直线平行的充分条件， 即：如果两条直线的斜率相等，那么这两条直线一定平行。两条直线都平行于y轴时，两直线的斜率都不存在。如果两条直线垂直，那么斜率相乘就为-1。

两直线平行，斜率相等。斜率是表示一条直线（或曲线的切线）关于（横）坐标轴倾斜程度的量。它通常用直线（或曲线的切线）与（横）坐标轴夹角的正切，或两点的纵坐标之差与横坐标之差的比来表示。两直线平行，斜率相等。

换句话说，如果两条直线的斜率不相等，那么它们一定不平行。因此，我们可以通过比较两条直线的斜率来确定它们是否平行。设两条直线的斜率分别为k1和k2，如果k1=k2，那么这两条直线平行；如果k1≠k2，那么这两条直线不平行。

如果两直线平行,那么它们的斜率关系是怎样的?

1、两直线平行，它们的斜率相等。斜率，亦称“角系数”，表示一条直线相对于横轴的倾斜程度。一条直线与某平面直角坐标系横轴正半轴方向的夹角的正切值即该直线相对于该坐标系的斜率。

2、两直线平行，斜率相等。斜率是表示一条直线（或曲线的切线）关于（横）坐标轴倾斜程度的量。它通常用直线（或曲线的切线）与（横）坐标轴夹角的正切，或两点的纵坐标之差与横坐标之差的比来表示。两直线平行，斜率相等。

3、它们的斜率相同。因为两条平行直线的斜率必须相等，才能保证它们在平面上不会相交。换句话说，如果两条直线的斜率不相等，那么它们一定不平行。因此，我们可以通过比较两条直线的斜率来确定它们是否平行。

4、平行直线是位于同一平面中的两条不相交且方向相同的直线，它们在坐标系中会平行且距离相等。由于直线的斜率可以表示为直线上的任意两点的坐标之差的比值，因此，两条平行直线的斜率相等。

5、两条直线的斜率相等是两条直线平行的充分条件， 即：如果两条直线的斜率相等，那么这两条直线一定平行。两条直线都平行于y轴时，两直线的斜率都不存在。如果两条直线垂直，那么斜率相乘就为-1。

6、当两直线平行时，它们的斜率之间的关系可以用以下公式表示：K1+K2=0。这个公式的含义是，如果两条直线分别与x轴正方向平行，那么它们的斜率之间的关系就是它们的斜率之和为零。

The End