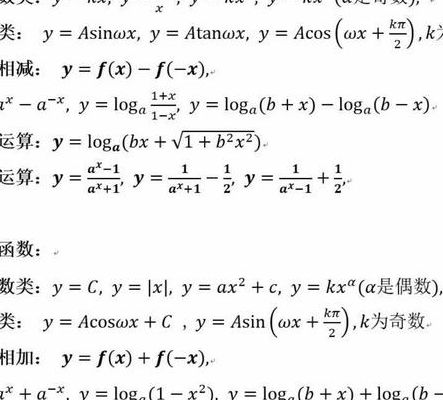什么是奇函数什么是偶函数（什么叫做奇函数什么叫做偶函数）

什么叫奇函数,什么叫偶函数

1、奇函数关于原点对称，偶函数关于y轴对称。两者的概念：奇函数是指对于一个定义域关于原点对称的函数f（x）的定义域内任意一个x，都有f（-x）= - f（x），那么函数f（x）就叫做奇函数（odd function）。

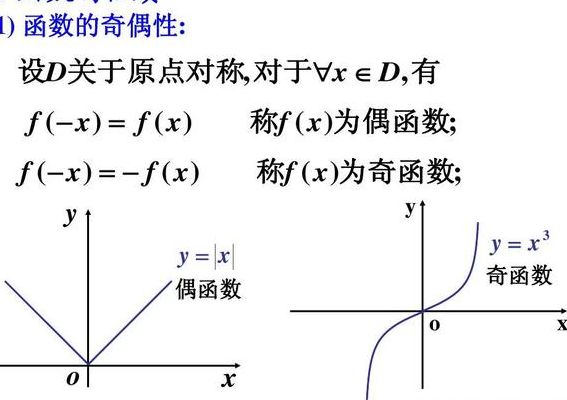
2、奇函数：如果对于函数f(x)的定义域内任意一个x，都有f(-x)= - f(x)，那么函数f(x)就叫做奇函数。偶函数：如果对于函数f(x)的定义域内任意一个x，都有f(-x)= f(x)，那么函数f(x)就叫做偶函数。

3、奇函数和偶函数判断如下 定义上来看：一般地，如果对于函数f(x)的定义域内任意一个x，都有f(-x）=f(x)，那么函数f(x)就叫偶函数。

4、奇函数是指对于一个定义域关于原点对称的函数f（x）的定义域内任意一个x，都有f（-x）= - f（x），那么函数f（x）就叫做奇函数（odd function）。

5、偶函数是关于y轴对称的，奇函数是关于原点对称的。一般地，如果对于函数f(x)的定义域内任意的一个x，都有f(x)=f(-x)，那么函数f(x)就叫做偶函数(Even Function)。

哪些是奇函数哪些是偶函数

正弦函数（y=sinx)是奇函数。正切函数（y=tanx)是奇函数。余切函数（y=cotx)是奇函数。余割函数（y=cscx)是奇函数。反比例函数是奇函数。f(x)=kx是奇函数。f(x)=x^a，其中a为奇数。

个典型奇偶函数是：正弦函数、正切函数、余切函数、余割函数、反比例函数、f(x)=kx、f(x)=x^a、双曲正弦函数伟奇函数。正弦函数（y=sinx)是奇函数。正切函数（y=tanx)是奇函数。余切函数（y=cotx)是奇函数。

常见的奇函数：sinx，tanx，1/x，arcsinx，arctanx，x^2n+1等。 常见的偶函数：lxl，cosx，x^2n(n为正整数)，e^lxl，e的x方等。

什么是奇偶函数?举例说明

函数的奇偶性是指函数在定义域内满足一定条件的对称性质。一个函数如果既是奇函数又是偶函数，那么它在原点附近具有两种对称性，即关于y轴和关于原点的对称性。

奇函数： sin(x) - 正弦函数是一个奇函数，满足 sin(-x) = -sin(x)。图像关于原点对称。 x^3 - x 的立方是一个奇函数，满足 f(-x) = -(f(x))。图像关于原点对称。

f(-x)=-f(x)的函数叫做奇函数。例如：y=x（y等于x的3次方）奇函数图象关于原点（0，0）对称。奇函数的定义域必须关于原点（0，0）对称，否则不能成为奇函数。

个典型奇偶函数有：正弦函数（y=sinx)是奇函数。正切函数（y=tanx)是奇函数。余切函数（y=cotx)是奇函数。余割函数（y=cscx)是奇函数。反比例函数是奇函数。f(x)=kx是奇函数。

奇函数是指对于一个定义域关于原点对称的函数f（x）的定义域内任意一个x，都有f（-x）= - f（x），那么函数f（x）就叫做奇函数（odd function）。

函数奇偶性的证明方法一般有：⑴定义法：函数定义域是否关于原点对称，对应法则是否相同。

什么是奇偶函数?有哪些?

1、奇函数： sin(x) - 正弦函数是一个奇函数，满足 sin(-x) = -sin(x)。图像关于原点对称。 x^3 - x 的立方是一个奇函数，满足 f(-x) = -(f(x))。图像关于原点对称。

2、奇函数是指对于一个定义域关于原点对称的函数f(x)的定义域内任意一个x，都有f(x)= - f(x)，那么函数f(x)就叫做奇函数。

3、函数的奇偶性是指函数在定义域内满足一定条件的对称性质。一个函数如果既是奇函数又是偶函数，那么它在原点附近具有两种对称性，即关于y轴和关于原点的对称性。

4、奇函数是指对于一个定义域关于原点对称的函数f（x）的定义域内任意一个x，都有f（-x）= - f（x），那么函数f（x）就叫做奇函数（odd function）。

什么是奇函数和偶函数?

1、首先定义域是R，且f(－x)=－f(x)，则此函数是奇函数； 如：f(x)=x ＋1，定义域是R，且f(－x)=f(x)，则此函数是偶函数。

2、奇函数和偶函数判断如下 定义上来看：一般地，如果对于函数f(x)的定义域内任意一个x，都有f(-x）=f(x)，那么函数f(x)就叫偶函数。

3、奇函数：如果对于函数f(x)的定义域内任意一个x，都有f(-x)= - f(x)，那么函数f(x)就叫做奇函数。偶函数：如果对于函数f(x)的定义域内任意一个x，都有f(-x)= f(x)，那么函数f(x)就叫做偶函数。

什么是奇函数偶函数

1、奇函数是指对于一个定义域关于原点对称的函数f（x）的定义域内任意一个x，都有f（-x）= - f（x），那么函数f（x）就叫做奇函数（odd function）。

2、奇偶函数是指：奇函数是指对于一个定义域关于原点对称的函数f（x），有f（-x）=-f（x），那么函数f（x）就叫做奇函数。奇函数在对称区间上的积分为零。

3、奇函数关于原点对称，偶函数关于y轴对称。两者的概念：奇函数是指对于一个定义域关于原点对称的函数f（x）的定义域内任意一个x，都有f（-x）= - f（x），那么函数f（x）就叫做奇函数（odd function）。

4、差）是奇函数；两个偶函数的和（差）是偶函数；奇函数与偶函数的和（差）既非奇函数也非偶函数；两个奇函数的积（商）为偶函数；两个偶函数的积（商）为偶函数；奇函数与偶函数的积（商）是奇函数。

5、一般地，如果对于函数f(x)的定义域内任意的一个x，都有f(x)=f(-x)，那么函数f(x)就叫做偶函数(Even Function)。性质 两个奇函数相加所得的和或相减所得的差为奇函数。

The End