卷积的物理意义（卷积的物理意义信号和函数等同）

信号卷积的物理意义

1、信号卷积在物理意义当中的意思就是说，当信号发射出去之后，发生一定的波的传输过程，有阻碍物遮挡而进行发生改变。

2、在信号处理中，卷积积分可以用来描述一个系统对输入信号的响应。具体来说，输入信号与系统响应之间进行卷积操作可以得到输出信号，即输出信号是输入信号在系统响应下的卷积积分。

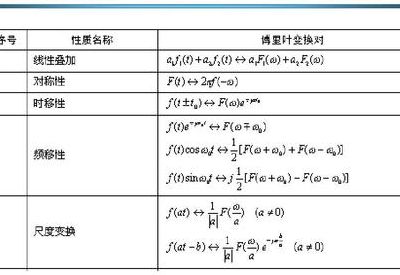
3、卷积公式卷积的物理意义是将输入信号用时移加权的单位冲激信号和（积分）表示，然后输出就是各个冲激信号作用系统后再求和，而时移量u（f(t-u)），再对u积分，就产生了反转。

4、卷积的物理意义：卷积可代表某种系统对某个物理量或输入的调制或污染。

5、卷积的物理意义是将输入信号用时移加权的单位冲激信号和（积分）表示，然后输出就是各个冲激信号作用系统后再求和，而时移量u（f（t-u）），再对u积分，就产生了反转。

有人能告诉我卷积和、卷积积分的物理意义,谢谢,诸位!

1、卷积积分的物理意义：在激励条件下，线性电路在t时刻的零状态响应=从激励函数开始作用的时刻（ξ=0）；到t时刻（ ξ=t）的区间内，无穷多个强度不同的冲激响应的总和。可见，冲激响应在卷积中占据核心地位。

2、系统对信号的响应和物理量的平均值。在信号处理中，卷积积分可以用来描述一个系统对输入信号的响应。具体来说，输入信号与系统响应之间进行卷积操作可以得到输出信号，即输出信号是输入信号在系统响应下的卷积积分。

3、问题一：卷积积分的物理意义 在激励条件下，线性电路在t时刻的零状态响应=从激励函数开始作用的时刻（ξ=0）到t时刻（ ξ=t）的区间内，无穷多个强度不同的冲激响应的总和。可见，冲激响应在卷积中占据核心地位。

4、卷积的物理意义：卷积可代表某种系统对某个物理量或输入的调制或污染。

5、卷积是分析数学中一种重要的运算。设f（x）， g（x）是R1上的两个可积函数，作积分：可以证明，关于几乎所有的x∈（－∞，∞） ，上述积分是存在的。

卷积公式的假定?

卷积的物理意义是将输入信号用时移加权的单位冲激信号和（积分）表示，然后输出就是各个冲激信号作用系统后再求和，而时移量u（f（t-u）），再对u积分，就产生了反转。

卷积公式是：z（t）=x（t）*y（t）=∫x（m）y（t-m）dm。这是一个定义式。卷积公式是用来求随机变量和的密度函数（pdf）的计算公式。

卷积计算公式为：N=(W-F+2P)/S+1。其中N表示输出大小，W表示输入大小，F表示卷积核大小，P表示填充值的大小，S表示步长大小。卷积的应用：统计学中，加权的滑动平均是一种卷积。

卷积公式

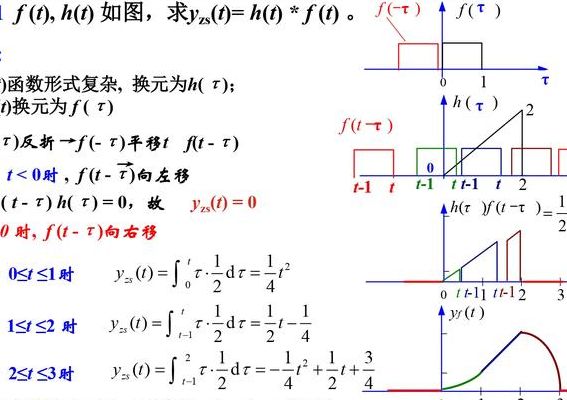
1、卷积公式为：f(t)g(t)=∫t0f(u)g(tu)du。卷积（Convolution)是通过两个函数f(t)和g(t)生成第三个函数的一种数学算子，表征函数f(t)与g(t)经过翻转和平移的重叠部分的面积。

2、卷积公式如下：卷积积分公式是（f *g）∧（x）=(x)·(x)，卷积是分析数学中一种重要的运算。设f（x）， g（x）是R1上的两个可积函数，作积分，可以证明，关于几乎所有的x∈（－∞，∞） ，上述积分是存在的。

3、卷积的计算公式和步骤如下：计算公式 f（t）*g（t）=∫f（τ）g（t-τ）dτ。步骤 对函数f（t）和g（t）进行离散化处理，变为离散信号。

4、卷积计算公式为：N=（W-F+2P）/S+1。其中N表示输出大小，W表示输入大小，F表示卷积核大小，P表示填充值的大小，S表示步长大小。卷积是一种线性运算，图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。

线性卷积的物理意义

1、卷积是一种积分运算，它可以用来描述线性时不变系统的输入和输出的关系：即输出可以通过输入和一个表征系统特性的函数（冲激响应函数）进行卷积运算得到。

2、问题一：卷积积分的物理意义 在激励条件下，线性电路在t时刻的零状态响应=从激励函数开始作用的时刻（ξ=0）到t时刻（ ξ=t）的区间内，无穷多个强度不同的冲激响应的总和。可见，冲激响应在卷积中占据核心地位。

3、卷积积分的物理意义：在激励条件下，线性电路在t时刻的零状态响应=从激励函数开始作用的时刻（ξ=0）；到t时刻（ ξ=t）的区间内，无穷多个强度不同的冲激响应的总和。可见，冲激响应在卷积中占据核心地位。

4、线性卷积是在时域描述线性系统输入和输出之间关系的一种运算。这种运算在线性系统分析和信号处理中应用很多，通常简称卷积。两个函数的圆周卷积是由他们的周期延伸所来定义的。

5、信号处理：卷积是信号处理中的基本运算之一，用于描述线性时不变系统的输入和输出之间的关系。例如，在图像处理中，卷积可以用来进行滤波、边缘检测等操作。

6、简单的说，线性卷积表示一个信号通过一个系统的输出，这个信号可以是无限长的，也可以是有限长的，可以的离散的也可以是连续的。

卷积积分公式是什么?

1、卷积积分公式是（f *g）∧（x）=(x)·(x)。卷积是分析数学中一种重要的运算。设f（x），g（x）是R1上的两个可积函数，作积分，可以证明，关于几乎所有的x∈（－∞，∞），上述积分是存在的。

2、卷积公式是：z（t）=x（t）*y（t）=∫x（m）y（t-m）dm。卷积是分析数学中一种重要的运算。设f（x）， g（x）是R1上的两个可积函数，作积分：可以证明，关于几乎所有的x∈（－∞，∞） ，上述积分是存在的。

3、卷积公式是：z(t)=x(t)*y(t)=∫x(m)y(t-m)dm。分析数学中一种重要的运算，设f（x）， g（x）是R1上的两个可积函数，作积分可以证明，关于几乎所有的x∈（－∞，∞） ，上述积分是存在的。

4、卷积积分公式是（f *g）∧（x）=(x)·(x)，卷积是分析数学中一种重要的运算。设f（x）， g（x）是R1上的两个可积函数，作积分，可以证明，关于几乎所有的x∈（－∞，∞） ，上述积分是存在的。

5、卷积的计算公式和步骤如下：计算公式 f（t）*g（t）=∫f（τ）g（t-τ）dτ。步骤 对函数f（t）和g（t）进行离散化处理，变为离散信号。

6、卷积的公式是f(t)g(t)=∫t0f(u)g(tu)du(1)。卷积公式与拉普拉斯变换结果的关系为：F(s)G(s)=∫∞0est(f(t)g(t))dt(3)。

The End