判断收敛和发散技巧（判断收敛和发散技巧的方法）

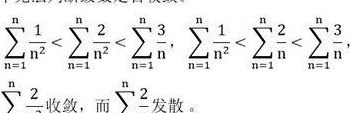
如何判断数列是收敛还是发散

比较法 将待判断的数列与已知的收敛或发散的数列进行比较，来判断数列的收敛或发散性。

直接计算：如果数列或函数序列的极限可以直接计算出来，那么就可以判断它是否发散。例如，数列 {1/n}（n从1到无穷大）的极限是0，因此它是收敛的。

极限法：利用极限的定义来判断数列的收敛和发散。如果当n→∞时，有liman=A，那么这个数列就是收敛的；如果当n→∞时，liman≠A，那么这个数列就是发散的。

极限定义法：极限定义法是判断数列收敛最基本的方法。它是通过观察数列中元素逐渐接近一个特定的值来判断数列的收敛性。

如何判断一个函数级数是否发散呢?

1、判断单调性：如果函数单调递增或者单调递减，并且无界，则函数发散。如果函数单调递增或者单调递减，并且有界，则函数收敛。判断极限：如果函数的极限存在且有限，则函数收敛。如果函数的极限不存在或者是无穷大，则函数发散。

2、判断函数收敛或发散的方法有定义法、极限法、导数法和判别法。定义法：对于数列而言，如果数列的每一项都收敛到一个确定的数，那么这个数列就是收敛的。

3、比较审敛法，和∑1/n比较，∑1/n发散，1/lnn＞∑1/n，所以原函数发散。

4、判定级数的发散性方法如下：看通项un的极限是不是0。如果极限不为0，那么∑un必然发散。如果极限为0，那么∑un就有可能发散也有可能收敛，要具体分析。

5、收敛和发散的判断：判断单调性 如果函数单调递增或者单调递减，并且无界，则函数发散。如果函数单调递增或者单调递减，并且有界，则函数收敛。判断极限 如果函数的极限存在且有限，则函数收敛。

6、判别一个级数的发散性有如下步骤。看通项un的极限是不是0。如果极限不为0，那么∑un必然发散。如果极限为0，那么∑un就有可能发散也有可能收敛，要具体分析。

如何判断一个级数收敛或者发散?

以下是一些常见的判断方法： 直接计算：如果数列或函数序列的极限可以直接计算出来，那么就可以判断它是否发散。例如，数列 {1/n}（n从1到无穷大）的极限是0，因此它是收敛的。

比较判别法：设有两个正项级数a_n和b_n，若对于所有n都有0≤a_n≤b_n，且∑b_n收敛，则由比较判别法可知∑a_n也收敛；若∑b_n发散，则由比较判别法可知∑a_n也发散。

比值判别法：如果一个级数的通项的绝对值的比值趋于0，那么这个级数收敛。根值判别法：如果一个级数的通项的绝对值的根值趋于0，那么这个级数收敛。级数发散的口诀。

判断收敛发散的方法总结

收敛和发散的判断方法：判断单调性：如果函数单调递增或者单调递减，并且无界，则函数发散。如果函数单调递增或者单调递减，并且有界，则函数收敛。判断极限：如果函数的极限存在且有限，则函数收敛。

函数的收敛和发散可以通过极限定义、数列收敛准则、单调性与有界性、导数与微分等方法判断。极限定义：根据函数的极限定义，可以通过求出函数在某一点或区间的极限值来判断函数的收敛和发散。

极限判断法：计算函数的极限，极限存在且有限，函数收敛；极限不存在或为无穷大，函数发散。对于函数f(x)=1/x，当x趋于无穷大时，极限为0，函数收敛。而对于函数f(x)=x，当x趋于无穷大时，极限为无穷大，函数发散。

极限判别法：对于数列项数n趋于无穷时，若数列的极限能一直趋近于实数a，那么这个数列就是收敛的，找不到实数a的数列就是发散的。

证明数列收敛的八种方法如下：定义法 如果数列满足条件：对于任意正整数n，数列的第n项与第n+1项之差的绝对值小于正无穷小，那么这个数列就是收敛的。

The End