常见的勾股数（常见的勾股数口诀表）

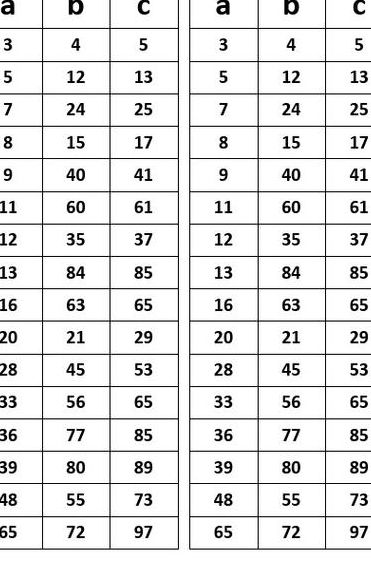
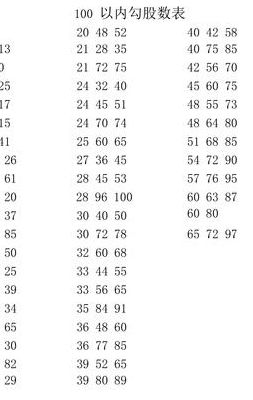
勾股定理常用的数字

1、常见组合：3，4，5 ： 勾三股四弦五 5，12，13 ： 5·21（12）记一生（13）6，8，10： 连续的偶数 特殊组合：连续的勾股数只有3，4，5 连续的偶数勾股数只有6，8，10 勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。

2、80 100 ；60 91 109 ； 63 84 105 ； 65 72 97 ； 66 88 110 ； 69 92 115 ；72 96 120 ； 75 100 125 ； 80 84 116。

3、②6，8，10 ③16 30 34 & 16 63 65等等。需要注意的是，勾股数有一点，必须是整数。依照原理，常用的勾股数莫过于最基本平常的勾三股四弦五了。可以构作直角三角形又是正整数的数字被人们统称为常用勾股数。

勾股数有哪些,有何特点?

1、勾股数又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股定理：直角三角形两条直角边a、b的平方和等于斜边c的平方（a+b=c）。勾股定理的日常应用：(1)理解方向角等概念，根据题意画出图形，利用定理或逆定理解决航海中距离问题。

2、特殊组合：连续的勾股数只有3，4，5 连续的偶数勾股数只有6，8，10 勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股定理：直角三角形两条直角边a、b的平方和等于斜边c的平方（a+b=c）。

3、勾股数指的是组成一个直角三角形的三条边长，三条边长都为正整数，例如直角三角形的两条直角边为a和b，斜边为c，那么两条直角边a的平方+b的平方等于斜边c的平方，那么这一组数组就叫做勾股数。一般把较短的直角边称为勾，较长直角边称为股，而斜边则为弦。

4、勾股数的特点是，它们之间存在一定的规律和性质。其中最为著名的性质就是勾股数之间的倍数关系。例如，5就是勾股数，而10则是5的倍数，也是勾股数。这个性质可以被用来寻找更多的勾股数。总之，勾股数是数学中一个非常重要的概念，它们的应用范围非常广泛。

5、n2+2n、2n2+2n+1，这可以通过勾股定理的逆定理获证。汇总：观察分析勾股数，可看出它们具有下列二个特点：直角三角形短直角边为奇数，另一条直角边与斜边是两个连续自然数。一个直角三角形的周长等于短直角边的平方与短边自身的和。

6、用特点1解：设这个直角三角形三边分别为1x、x+1，则有：169+x2=(x+1)2，解得x=84，此三角形周长=13+84+85=182。用特点2解：此直角三角形是以奇数为边构成的直角三角形，因此周长=169+13=182。

勾股数有哪些

1、，4，5 ： 勾三股四弦五 5，12，13 ： 5·21（12）记一生（13）6，8，10： 连续的偶数 特殊组合：连续的勾股数只有3，4，5 连续的偶数勾股数只有6，8，10 勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。

2、勾股数有：（3n、4n、5n）（n是正整数），这是最著名的一组，俗称“勾三，股四，弦五”。古人把较短的直角边称为勾，较长直角边称为股，而斜边则为弦。

3、常用的勾股数有：5；113；225；117；40、41等等。勾股数，又名毕氏三元数。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股数的依据是勾股定理。勾股定理是人类早期发现并证明的重要数学定理之一。

4、常见的勾股数有：（3，4，5），（6，8，10）……；3n，4n，5n（n是正整数）。勾股数，又名毕氏三元数。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股定理：直角三角形两条直角边a、b的平方和等于斜边c的平方（a+b=c）。

常见勾股数列表有?

常用的勾股数有：5；113；225；117；40、41等等。勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股数的依据是勾股定理。勾股定理是人类早期发现并证明的重要数学定理之一。

，12 ，13 7 ，24 ， 25 9 ，40 ，41 11，60 ，61 ……2n+1，2n+2n ，2n+2n+1 看一组数是否为勾股数，首先除去最大公约数，再看较大的两个数是否相差1，且较大的两数之和是最小数的平方。

常用的勾股数有：（5），（113），（225），（117），（40、41），（226），（160、61），（1337），（4573），（1120），（1885）。勾股数的定义 勾股数，又名毕氏三元数。

4 5 ，113 同时乘以倍数，比如。

①3，4，5勾三股四弦五 ②6，8，10 ③16 30 34 & 16 63 65等等。需要注意的是，勾股数有一点，必须是整数。依照原理，常用的勾股数莫过于最基本平常的勾三股四弦五了。可以构作直角三角形又是正整数的数字被人们统称为常用勾股数。

数学中常见的勾股数有哪些

1、②6，8，10 ③16 30 34 & 16 63 65等等。需要注意的是，勾股数有一点，必须是整数。依照原理，常用的勾股数莫过于最基本平常的勾三股四弦五了。可以构作直角三角形又是正整数的数字被人们统称为常用勾股数。

2、常用的勾股数有：5；113；225；117；40、41等等。勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股数的依据是勾股定理。勾股定理是人类早期发现并证明的重要数学定理之一。

3、（5）（10）（113）（117）（225）勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股定理：直角三角形两条直角边a、b的平方和等于斜边c的平方（a+b=c）。

4、常用的勾股数有：（5），（113），（225），（117），（40、41），（226），（160、61），（1337），（4573），（1120），（1885）。勾股数的定义 勾股数，又名毕氏三元数。

5、4 5 ，113 同时乘以倍数，比如。

常见的勾股数有哪些

4 5 ，113 同时乘以倍数，比如。

常见组合：3，4，5 ： 勾三股四弦五 5，12，13 ： 5·21（12）记一生（13）6，8，10： 连续的偶数 特殊组合：连续的勾股数只有3，4，5 连续的偶数勾股数只有6，8，10 勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。

，12 ，13 7 ，24 ， 25 9 ，40 ，41 11，60 ，61 ……2n+1，2n+2n ，2n+2n+1 看一组数是否为勾股数，首先除去最大公约数，再看较大的两个数是否相差1，且较大的两数之和是最小数的平方。

常用的勾股数有：5；113；225；117；40、41等等。勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股数的依据是勾股定理。勾股定理是人类早期发现并证明的重要数学定理之一。

常用的勾股数有：（5），（113），（225），（117），（40、41），（226），（160、61），（1337），（4573），（1120），（1885）。勾股数的定义 勾股数，又名毕氏三元数。

The End