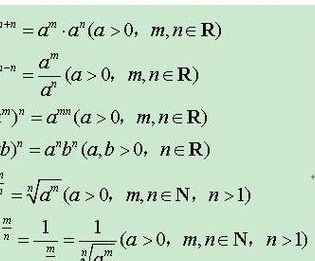指数函数公式（指数函数公式总结）

对数函数,指数函数,幂函数分别怎样计算?

1、对数函数：一般地，函数y=logax（a0，且a≠1）叫做对数函数，也就是说以幂（真数）为自变量，指数为因变量，底数为常量的函数，叫对数函数。指数函数：y=a^x，(a0且a≠1)幂函数：一般地.形如y=xα(α为有理数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。

2、指数函数的规律是f(x) = a^x，其中a为常数且大于0且不等于1。对数函数的规律是f(x) = log_a(x)，其中a为常数且大于0且不等于1。幂函数的规律是f(x) = x^a，其中a为常数。这三种函数都具有特定的增长或减少规律，可以用来描述各种自然现象和数学问题。

3、次方根与幂函数定义/当正偶数时，我们有算术平方根 sqrt[n](x)，如 sqrt(4) = 2，定义为非负实数。对于正奇数，如 sqrt[3](27)，是奇函数。推广到实数范围，非整数指数如 (1/2)^x，存在两个解，通常取正值。

4、①幂函数：y＝x^μ（μ≠0，μ为任意实数）定义域：μ为正整数时为（－∞，＋∞），μ为负整数时是（－∞，0）∪（0，＋∞）；μ＝(α为整数)，当α是奇数时为（ －∞，＋∞），当α是偶数时为（0，＋∞）；μ＝p／q，p，q互素，作为的复合函数进行讨论。略图如图图3。

5、你是想问幂函数、指数函数、对数函数的定理公式这个问题吧？其定理公式分别如下：一般地，y=xα（α为有理数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。例如函数y=x0、y=xy=xy=x-1（注：y=x-1=1/x、y=x0时x≠0）等都是幂函数。

6、理解有理指数幂的含义；了解实数指数幂的意义；掌握幂的运算；理解指数函数的概念和意义；理解指数函数的图象、单调性与特殊点。理解对数的概念及其运算性质；了解对数换底公式，能将一般对数转化成自然对数或常用对数；了解对数函数的概念；理解对数函数的图象、单调性与特殊点。

指数函数公式是什么?

1、指数函数公式：y=a^x(a为常数且以a0，a≠1)。函数的定义域是R。在指数函数的定义表达式中，在a^x前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式。指数函数基本性质：（1）指数函数的定义域为R，这里的前提是a大于0且不等于1。

2、公式：(x^a)=ax^(a-1)。证明：y=x^a取对数lny=alnx两边对x求导(1/y)*y=a/x所以y=ay/x=ax^a/x=ax^(a-1)y=a^x。两边取对数：lny=xlna两边同时对x求导数：==y/y=lna==y=ylna=a^xlna。指数函数：是数学中重要的函数。应用到值e上的这个函数写为exp(x)。

3、指数函数运算公式：a^m+n=a^ma^n。指数函数介绍如下：指数函数是重要的基本初等函数之一。一般地，y=a^x函数(a为常数且以a0，a≠1)叫做指数函数，函数的定义域是R，注意，在指数函数的定义表达式中，在a^x前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式。

4、指数函数公式：y=ax。指数函数是重要的基本初等函数之一。一般地，y=ax函数（a为常数且以a0，a≠1）叫做指数函数，函数的定义域是R。初等函数是由基本初等函数经过有限次的四则运算和复合运算所得到的函数。基本初等函数和初等函数在其定义区间内均为连续函数。

5、八个公式：y=c(c为常数) y=0；y=x^n y=nx^(n-1)；y=a^x y=a^xlna y=e^x y=e^x；y=logax y=logae/x y=lnx y=1/x ；y=sinx y=cosx ；y=cosx y=-sinx ；y=tanx y=1/cos^2x ；y=cotx y=-1/sin^2x。

指数函数运算法则

1、同底数相加减：对于两个底数相同的指数函数，可以将底数保持不变，同时将指数进行加减运算。例如，如果有两个指数函数f(x)=a^x和g(x)=a^y，其中a为常数，那么f(x)+g(x)=a^x+a^y，f(x)-g(x)=a^x-a^y。

2、乘法 同底数幂相乘，底数不变，指数相加。幂的乘方，底数不变，指数相乘。积的乘方，等于把积的每一个因式分别乘方，再把所得的幂相乘。分式乘方，分子分母各自乘方。除法 同底数幂相除，底数不变，指数相减。规定：（1）任何不等于零的数的零次幂都等于1。

3、数函数运算法则 （1）a^m+n=a^ma^n；（2）a^mn=(a^m)^n；（3）a^1/n=^n√a；（4）a^m-n=a^m/a^n。(1)指数函数的定义域为R，这里的前提是a大于0且不等于1。对于a不大于0的情况，则必然使得函数的定义域不连续，因此我们不予考虑，同时a等于0函数无意义一般也不考虑。

The End