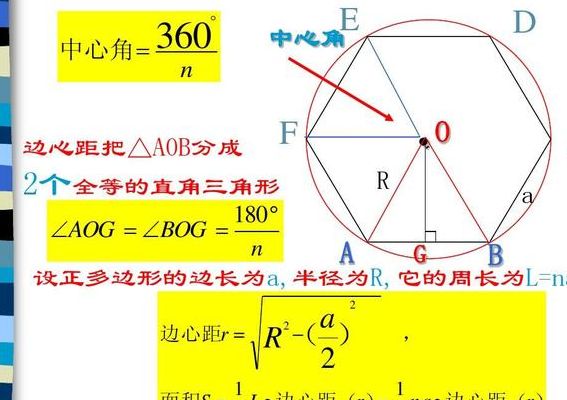
边心距是什么（六边形的边心距是什么）

边心距是什么意思

1、边心距是指边心距是指正多边形的每条边到其外接圆的圆心的距离..正六边形的边长就等于其内切圆的半径，它的边心距等于边长的√3/2倍. 三角形的边心距就是其内切圆的半径。正多边形的边心距就是其内切圆的半径。

2、相邻原子间的距离。根据查询相关公开信息显示，边心距是指晶体结构中一个晶胞中的相邻原子间的距离。在立方晶系中，边心距的值等于晶格常数a的414倍，在其他晶系中，边心距的值等于晶格常数a的根号2倍。

3、正多边形的边心距是正多边形的外接圆圆心（同时也是内切圆圆心）到正多边形某一边的距离。正多边形的边心距都相等，并等于其内切圆的半径。已知正多边形中心的情况下，边心距可通过从正多边形中心向某一边作垂线段；或连接正多边形中心和某一边的中点求得。

边心距是什么

1、边心距是指边心距是指正多边形的每条边到其外接圆的圆心的距离..正六边形的边长就等于其内切圆的半径，它的边心距等于边长的√3/2倍. 三角形的边心距就是其内切圆的半径。正多边形的边心距就是其内切圆的半径。正多边形都有的外接圆，每条边的中心角，实际上就是这条边所对的弧的圆心角。

4、等边三角形的边心距=高÷3=边长×2√3/3 等边三角形（又称正三边形），为三边相等的三角形，其三个内角相等，均为60°，它是锐角三角形的一种。等边三角形也是最稳定的结构。等边三角形是特殊的等腰三角形，所以等边三角形拥有等腰三角形的一切性质。

5、正多边形的中心到它的一边的距离叫做正多边形的边心距。正多边形的边心距等于正多边形的内切圆半径r。正多边形的正多边形才有中心，中心是正多边形内切圆或外接圆的圆心每一条边所对的外接圆的圆心角叫做正多边形的中心角正多边形的外接圆的半径叫做正多边形的半径。

等边三角形的边心距怎么求?公式是什么?

边长×√3/3。等边三角形的中心即为三角形的重心，连接重心与顶点到对边的线段被重心分成2：1的比例，而这条边恰好就是等边三角形的高，于是中心到顶点距离为高×三分之二。而高=边长×√3/2，于是中心到顶点距离为边长×√3/3。

以下是一些常见图形的边心距计算公式：矩形：如果矩形的宽度和高度已知，边心距可以计算为：边心距 = 矩形宽度 / 2。圆形：如果知道圆形的半径，边心距可以计算为：边心距 = 圆形半径。正三角形：如果知道正三角形的边长，边心距可以计算为：边心距 = 边长 / (2 * √3)。

等边三角形三心合一，三角都是60°，三点到重心的距离相等根据图形和勾股定理得d=√3/3 a。等边三角形（又称正三边形），为三边相等的三角形，其三个内角相等，均为60°，它是锐角三角形的一种。等边三角形也是最稳定的结构。

正多边形怎么求边心距？做其中两边的垂直平分线，得其交点是圆心。将各端点同圆心连起来，这就是半径R。正N多边形就有N条半径，每两条半径之间的夹角就是360/N。边长就是2Rsin(180/N)，边心距就是Rcos(180/N)。周长就是2NRsin(180/N)，面积就是NRsin(180/N)Rcos(180/N)。

设正三角形的边长为a，求正三角形的半径，边心距，面积。作高，则高平分边里用勾股定理可求得高=根号3a/2，正三角形的中心把高分为两部分，较长部分等于半径，较短部分等于边心距，且半径与边心距之比为2：1 所以半径= 根号3a/3，边心距= 根号3a/6，面积=根号3a/4。

如图：OB=3，则AB=3√3。边长=6√3，周长=18√3。

等边三角形的边心距是什么

等边三角形的边心距=高÷3=边长×√3/6 等边三角形（又称正三边形），为三边相等的三角形，其三个内角相等，均为60°，它是锐角三角形的一种。等边三角形也是最稳定的结构。等边三角形是特殊的等腰三角形，所以等边三角形拥有等腰三角形的一切性质。

边心距是指三角形每一边与所对的角的平分线所夹的角平分线上的点到该三角形的三边垂直平分线的交点的距离，在等边三角形中，边心距将三角形分成六个面积相等的小三角形，同时也等于这个等边三角形的高，且是内切圆半径，此外，边心距也可以通过三角形的半周长和一边来计算。

asd1113022786：您好。（1）等边三角形每个角为60° 中心角（圆心角）＝60°×2＝120° （2）cos30°＝0.86603 半径＝√3÷0.86603＝99999＝2 边心距＝√（2-3）＝√1＝1 周长＝2√3×3＝6√3 面积＝（1×√3）÷2×6＝3√3 是这样吗，祝好，再见。

等边三角形内心、外心、重心重合。内心到底边的距离也就是重心到底边的距离，也就是高的三分之一。如果等边三角形的边长为a，高就是√3/2a，内心到底边的距离就是√3a/6。

The End