平面与平面垂直的判定（平面与平面垂直的性质）

数学中两平面垂直的判定

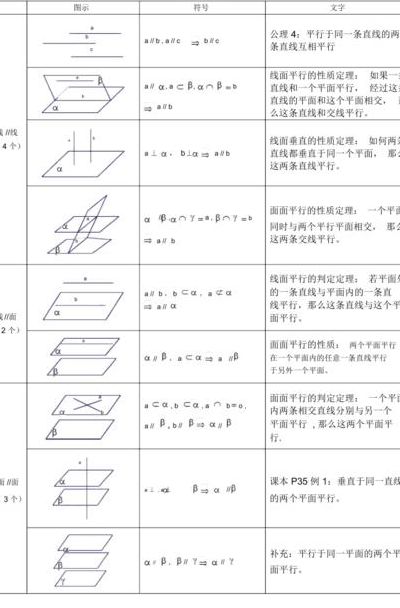
1、判定两平面垂直 定义法：如果两个平面所成的二面角为90°，那么这两个平面垂直。 判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。 如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。

2、如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。求解定理为，已知：α⊥β，α∩β=l，O∈l，OP⊥l，OPα。求证：OP⊥β。如果两个平面相互垂直，那么经过第一个平面内的一点作垂直于第二个平面的直线在第一个平面内。

3、判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。如果N个互相平行的平面有一个垂直于一个平面 那么其余平面均垂直这个平面。

平面与平面垂直的判定方法是什么

1、平面与平面垂直的判定方法如下：如果两个平面所成的二面角为90°，那么这两个平面垂直；如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直；如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。

2、(1)定义法：如果两个平面所成的二面角为90°，那么这两个平面垂直。(2)判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。(3)如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。

3、判定两平面垂直 定义法：如果两个平面所成的二面角为90°，那么这两个平面垂直。 判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。 如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。

4、平面与平面垂直的判定方法 定义法：如果两个平面所成的二面角为90°，那么这两个平面垂直。判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。

5、平面垂直于平面的判定是如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。如果N个互相平行的平面有一个垂直于一个平面，那么其余平面均垂直这个平面。

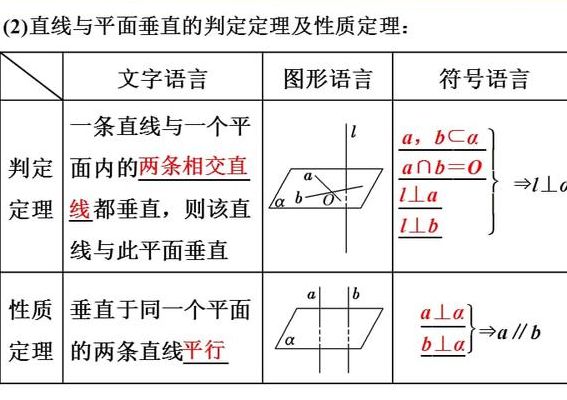
6、直线与平面垂直的判定定理（线面垂直定理）：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。推论1：如果在两条平行直线中，有一条直线垂直于一个平面，那么另一条直线也垂直于这个平面。推论2：如果两条直线垂直于同一个平面，那么这两条直线平行。

平面与平面垂直的判定定理

定理1：如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。定理2：如果两个平面相互垂直，那么经过第一个平面内的一点作垂直于第二个平面的直线在第一个平面内。定理3：如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面。

平面与平面垂直的判定定理是：如果一个平面内垂直于两个平面的交线的直线垂直于第三个平面，那么这三个平面相互垂直。如果平面α与平面β相交，且直线l垂直于两个平面的交线，那么当l垂直于第三个平面γ时，可以确定平面γ与α和β都垂直。证明这个定理并不难。

面面垂直的性质定理一共有四条，定理如下：如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。求解定理为，已知：α⊥β，α∩β=l，O∈l，OP⊥l，OPα。求证：OP⊥β。

怎样判断两个平面是否垂直?

1、(1)定义法：如果两个平面所成的二面角为90°，那么这两个平面垂直。(2)判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。(3)如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上，那么垂直。

2、如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。如果两个平面相互垂直，那么经过第一个平面内的一点作垂直于第二个平面的直线在第一个平面内。如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面。

3、(2)判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。

The End