抛物线焦点弦公式（抛物线焦点弦公式x1x2）

抛物线的焦点弦公式是?

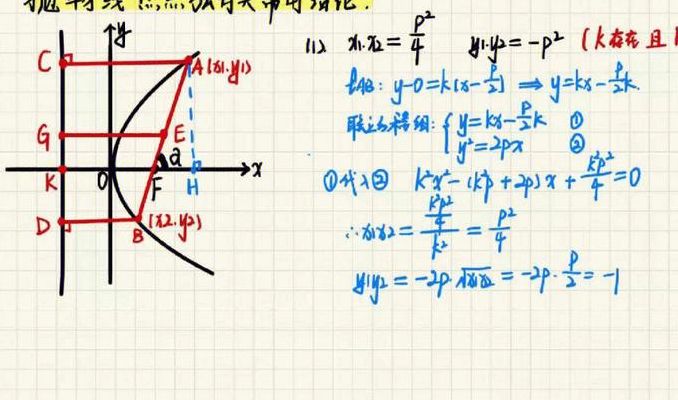
抛物线焦点弦长公式是2p/sina^2。设抛物线为y^2=2px(p0)，过焦点f(p/2，0)的弦直线方程为y=k(x-p/2)，直线与抛物线交于a（x1，y1)，b(x2，y2)。联立方程得k^2(x-p/2)^2=2px，整理得k^2x^2-p(k^2+2)x+k^2p^2/4=0。所以，x1+x2=p(k^2+2)/k^2。

抛物线的焦点弦公式为：2p/sin^2a。抛物线的焦点弦公式是一个描述抛物线焦点与弦长之间关系的公式。对于任意一个抛物线，其焦点到曲线上任意一点的距离之和为固定值，这个固定值等于焦点到该抛物线的准线的距离。这个性质可以用数学公式表达为：焦点到曲线上任意一点的距离等于该点到准线的距离。

抛物线焦点弦公式是：2p/sin^2（a）。抛物线焦点弦公式是抛物线几何性质的一个重要体现，反映了过焦点的弦与抛物线参数之间的关系。在标准形式的抛物线y^2=2px（p；0）中，焦点为f（p/2，0），准线为x=-p/2。过焦点的弦ab的直线方程可以设为y=k（x-p/2），其中k为直线的斜率。

抛物线焦点弦长公式是：2p/sina^2。抛物线焦点弦的性质焦点弦两端点处的两条切线相交在准线上，并且该交点与焦点的连线垂直于这条焦点弦。反过来，过准线上任意一点作圆锥曲线的两条切线，连接这两个切线的直线将通过焦点。以焦点弦为直径的圆与相应准线的关系：椭圆相离；双曲线相交；抛物线相切。

焦点弦公式是什么?

ecosθ=λ-1/λ+1这叫焦点弦公式，在椭圆、双曲抛物线中都有这个公式，如抛物线中：FA=p/(1-cosθ) FB=p/(1+cosθ) 可见这个是问题中e*cosθ=|（1-λ）/(1+ λ) | (λ=AF/BF，θ为与坐标轴夹角)的一个推论。

焦点弦公式2p/sina^2。证明：设抛物线为y^2=2px(p0)，过焦点f(p/2，0)的弦直线方程为y=k(x-p/2)，直线与抛物线交于a（x1，y1)，b(x2，y2)联立方程得k^2(x-p/2)^2=2px，整理得k^2x^2-p(k^2+2)x+k^2p^2/4=0。所以，x1+x2=p(k^2+2)/k^2。

焦点弦公式2p/sina^2。抛物线是指平面内与一定点和一定直线（定直线不经过定点）的距离相等的点的轨迹，其中定点叫抛物线的焦点，定直线叫抛物线的准线。它有许多表示方法，例如参数表示，标准方程表示等等。 它在几何光学和力学中有重要的用处。

在y=2px中，过焦点直线交抛物线于A(x1，y1)和B(x2，y2)两点，则AB弦长：d=p+x1+x2，图形关于x轴对称，焦点为（p/2，0）。

抛物线焦点弦长公式是什么呢?

1、抛物线焦点弦长公式是2p/sina^2。设抛物线为y^2=2px(p0)，过焦点f(p/2，0)的弦直线方程为y=k(x-p/2)，直线与抛物线交于a（x1，y1)，b(x2，y2)。联立方程得k^2(x-p/2)^2=2px，整理得k^2x^2-p(k^2+2)x+k^2p^2/4=0。所以，x1+x2=p(k^2+2)/k^2。

2、抛物线过焦点的弦长公式为：2p/sina^2。设抛物线方程为y^2=2px，焦点为（p，0），准线为x=-p。设过焦点的弦为AB，其方程为y=k（x-p），其中k≠0。将该方程代入抛物线方程，得到k^2x^2-（2p+2pk^2）x+p^2k^2=0。设两交点为A（x1，y1），B（x2，y2）。

3、焦点弦公式2p/sina^2。证明：设抛物线为y^2=2px(p0)，过焦点f(p/2，0)的弦直线方程为y=k(x-p/2)，直线与抛物线交于a（x1，y1)，b(x2，y2)。联立方程得k^2(x-p/2)^2=2px，整理得k^2x^2-p(k^2+2)x+k^2p^2/4=0，所以，x1+x2=p(k^2+2)/k^2。

4、抛物线弦长公式如下：在抛物线y？=2px中，弦长公式为d=p+x1+x2。在抛物线y？=-2px中，d=p-(x1+x2)。在抛物线x？=2py中，弦长公式为d=p+y1+y2。在抛物线x？=-2py中，弦长公式为d=p-(y1+y2)。

5、几何领域的抛物线焦点弦弦长公式 定义：如果一条倾斜角为α的直线过抛物线焦点F，并交抛物线于A。

抛物线焦点弦公式是什么?

1、抛物线焦点弦长公式是2p/sina^2。设抛物线为y^2=2px(p0)，过焦点f(p/2，0)的弦直线方程为y=k(x-p/2)，直线与抛物线交于a（x1，y1)，b(x2，y2)。联立方程得k^2(x-p/2)^2=2px，整理得k^2x^2-p(k^2+2)x+k^2p^2/4=0。所以，x1+x2=p(k^2+2)/k^2。

2、抛物线焦点弦长等于两交点到准线的距离之和，等于两交点相应坐标之和绝对值加P。

3、抛物线焦点弦公式是：2p/sin^2（a）。抛物线焦点弦公式是抛物线几何性质的一个重要体现，反映了过焦点的弦与抛物线参数之间的关系。在标准形式的抛物线y^2=2px（p；0）中，焦点为f（p/2，0），准线为x=-p/2。过焦点的弦ab的直线方程可以设为y=k（x-p/2），其中k为直线的斜率。

4、抛物线焦点弦长公式是：2p/sina^2。抛物线焦点弦的性质焦点弦两端点处的两条切线相交在准线上，并且该交点与焦点的连线垂直于这条焦点弦。反过来，过准线上任意一点作圆锥曲线的两条切线，连接这两个切线的直线将通过焦点。以焦点弦为直径的圆与相应准线的关系：椭圆相离；双曲线相交；抛物线相切。

动量守恒定律实验

1、验证动量守恒定律实验是要验证的是方程：m1·OP=m1·OM +m2·ON是否成立。动量是矢量，必须说明方向；在用动量守恒定律解题时，要规定好正方向。动量守恒定律是自然界中最普遍的守恒定律之一，它既适用于宏观的巨大物体，也适用于微观粒子；既可用在低速运动的物体上，也适用于高速运转的物体。

2、(2)当所测物理量满足___时(用所测物理量的字母表示)，即说明两球碰撞遵守动量守恒定律。

3、动量守恒定律公式为：m1*v1+m2*v2=m1*v1+m2*v2(式2)在本实验中，我们可以假设小球B的质量为m2，撞击过程中小球B的速度为v2，小球A的速度为v1，撞击后小球B的速度为v2，小球A的速度为v1。

4、根据动量守恒定律的适用条件，上述实验成功的关键在于：入射小球质量大于被碰小球，要确保对心碰撞后被碰小球做平抛运动，入射小球碰撞前速度恒定。因此，可知在上述实验中主要做了如下近似，斜面近似为光滑斜面、碰撞近似为完全弹性对心碰撞，并且严格来说应不计空气阻力。

5、动量守恒定律：如果物体系受到的合外力为零，则系统内各物体动量的矢量和保持不变，系统质心维持原本的运动状态。牛顿摆是一个1960年代发明的桌面演示装置，五个质量相同的球体由吊绳固定，彼此紧密排列。牛顿摆是由法国物理学家埃德姆·马略特（Edme Mariotte）最早于1676年提出的。

The End