三角形中线公式（三角形中线公式推导）

三角形中线定理公式

1、定理内容：三角形一条中线两侧所对边平方的和等于底边的平方的一半加上这条中线的平方的2倍。即，对任意三角形△ABC，设是I线段BC的中点，AI为中线，则有如下关系：AB+AC=2BI+2AI或作AB+AC=1/2BC+2AI。

2、定理内容 三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。

3、AB2+AC2=2BI2+2AI2或作AB2+AC2=（1/2）BC+2AI定理提出者 古希腊几何学家、天文学家阿波罗尼(奥)斯是欧几里得的门徒，他对几何学的醒目贡献是把欧几里得的《圆锥曲线》完善为新专著《圆锥曲线论》；他提出的“中线定理”， 迄今也有实用价值。

4、中线定理公式：AB2+AC2=2BI2+2AI2。中线介绍如下：中线是三角形中从某边的中点连向对角的顶点的线段。三角形的三条中线总是相交于同一点，这个点称为三角形的重心，重心分中线为2：1（顶点到重心：重心到对边中点）。

5、对任意三角形△ABC，设I是线段BC的中点，AI为中线，则有如下关系：AB+AC=2(BI+AI)或作AB+AC=1/2（BC）+2AI，中线定理，又称阿波罗尼奥斯定理，是欧氏几何的定理，表述三角形三边和中线长度关系。

6、三角形中线长定理公式是2（m^2+n^2）=a^2+b^2。中线长定理，是表述三角形三边和中线长度关系的定理，具体是指三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。三角形的中线是连接三角形的一个顶点及其对边中点的线段，一个三角形有3条中线。

三角形中线长定理公式

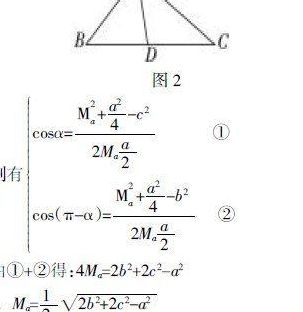
1、AB2+AC2=2BI2+2AI2 或作AB2+AC2=（1/2）BC+2AI。定理证明 如图，AD是△ABC的中线，AH是高线。

2、中线长定理公式是AD^2＝(b^2×u+c^2×v)/a-uv，中线定理是一种数学原理，指的是三角形一条中线两侧所对的边平方和等于底边平方的一半与该边中线平方的两倍的和。中线定理又称重心定理，是欧氏几何的定理，表述三角形三边和中线长度关系。

3、中线定理，又称重心定理，是欧氏几何的定理，表述三角形三边和中线长度关系。定理内容：三角形一条中线两侧所对边平方的和等于底边一半的平方加上这条中线的平方的和的2倍。

中线公式是什么?

中线公式是Sa＝√[(2b)+(2c)-a]。中线定理是一种数学原理，指的是三角形一条中线两侧所对的边平方和等于底边平方的一半与该边中线平方的两倍的和。中线定理（pappus定理），又称重心定理，是欧氏几何的定理，表述三角形三边和中线长度关系。

中线长公式是2（m^2+n^2）=a^2+b^2 资料扩展 中线长定理是阿波罗尼奥斯提出的一种在三角形中，求解中线长度的术语，适用于数学领域。定理定义 中线长定理 是表述三角形三边和中线长度关系的定理，具体是指三角形一条中线两侧所对边平方和等于底边的一半平方与该边中线平方和的2倍。

中线长公式主要指的是三角形中线的长度计算公式，具体地，中线长定理公式是：三角形中线的长度等于三角形一边长的一半与该边所对的高之和。其中，中线是三角形中从某边的中点连向对角的顶点的线段。

中线定理公式：AB2+AC2=2BI2+2AI2。中线介绍如下：中线是三角形中从某边的中点连向对角的顶点的线段。三角形的三条中线总是相交于同一点，这个点称为三角形的重心，重心分中线为2：1（顶点到重心：重心到对边中点）。

The End