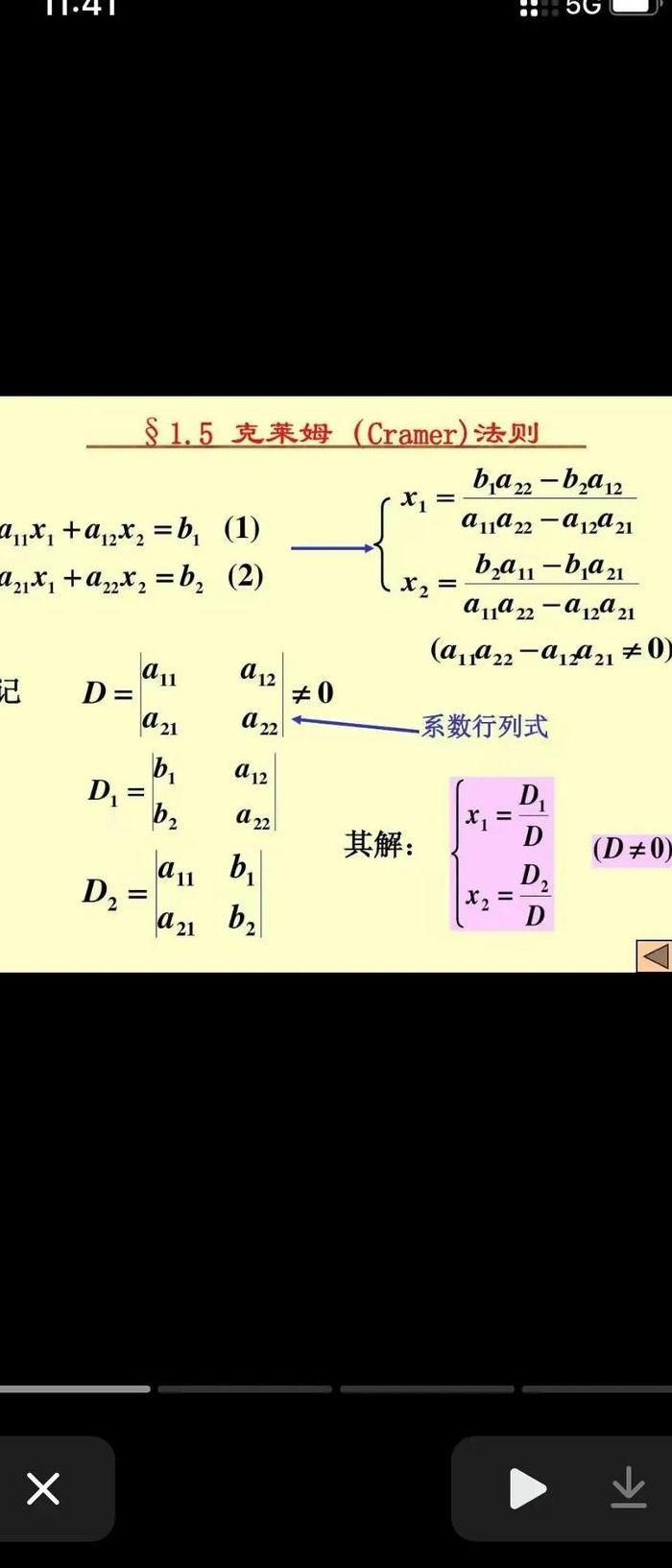
克莱姆法则（克莱姆法则零解算唯一解吗）

如何理解克莱姆法则

克拉默法则理解如下：克莱姆法则，又译克拉默法则(CramersRule)是线性代数中一个关于求解线性方程组的定理。它适用于变量和方程数目相等的线性方程组，是瑞士数学家克莱姆(1704-1752)于1750年，在他的《线性代数分析导言》中发表的。

克莱姆法则研究了方程组的系数与方程组解的存在性与唯一性关系。

克莱姆法则：是将方程组等式右侧的向量，替换到系数矩阵的第几行，得到新的行列式。

把系数写成矩阵A，右边常数写成矩阵b，求解Ax=b即可，具体为：x=(AA)-1(Ab)先定义所要相乘的矩阵，如A、B且要满足，A矩阵的列数等于B矩阵，这时两个矩阵相乘才有意义。此时定义的运算是A*B，不能颠倒乘法顺序；颠倒后结果亦不同。

克莱姆法则〔Cramers Rule〕是瑞士数学家克莱姆〔1704-1752〕於1750年，在他的《线性代数分析导言》中发表的。

克拉默法则公式是什么?

1、克拉姆法则公式是假若有a11X1+a12X2+...+a1nXn=b1，a21X1+a22X2+...+a2nXn=b2，an1X1+an2X2+...+annXn=bn。克莱姆法则的重要理论价值：研究了方程组的系数与方程组解的存在性与唯一性关系；应用克莱姆法则判断具有N个方程、N个未知数的线性方程组的解。

2、克拉默法则解方程组过程如下：先求系数行列式，再求各未知数对应的行列式，相除得到方程的解。克莱姆法则，又译克拉默法则是线性代数中一个关于求解线性方程组的定理。它适用于变量和方程数目相等的线性方程组，是瑞士数学家克莱姆（1704-1752）于1750年。在他的《线性代数分析导言》中发表的。

3、线性代数克拉默法则公式：在n元线性方程组中，如果系数矩阵为A，未知向量为x，常数向量为b，则该方程组可以表示为Ax=b。法则简介：克莱姆法则，又译克拉默法则（Cramers Rule）是线性代数中一个关于求解线性方程组的定理。

4、克拉默法则公式：a21=x1。克拉默法则是线性代数中的一种求解线性方程组的方法。适用范围：克拉默法则主要适用于方程组的系数矩阵为方阵的情况。对于一个n个未知数的线性方程组，其系数矩阵为A，常数向量为b，未知数向量为x，可以表示为Ax=b。核心思想：克拉默法则的核心思想是利用行列式的性质求解未知数。

5、对于多于两个或三个方程的系统，克莱姆的规则在计算上非常低效；与具有多项式时间复杂度的消除方法相比，其渐近的复杂度为O（n·n！）。即使对于2×2系统，克拉默的规则在数值上也是不稳定的。相关信息：一般来说，用克莱姆法则求线性方程组的解时，计算量是比较大的。

克莱默法则是什么?

1、克莱姆法则，又译克拉默法则（Cramers Rule）是线性代数中一个关于求解线性方程组的定理。当方程组的系数行列式不等于零时，则方程组有解，且具有唯一的解；如果方程组无解或者有两个不同的解，那么方程组的系数行列式必定等于零克莱姆法则不仅仅适用于实数域，它在任何域上面都可以成立。

2、克莱姆法则，又译克拉默法则（Cramers Rule）是线性代数中一个关于求解线性方程组的定理。它适用于变量和方程数目相等的线性方程组，是瑞士数学家克莱姆（1704-1752）于1750年，在他的《线性代数分析导言》中发表的。其实莱布尼兹〔1693〕，以及马克劳林〔1748〕亦知道这个法则，但他们的记法不如克莱姆。

3、克拉默法则解方程组过程如下：先求系数行列式，再求各未知数对应的行列式，相除得到方程的解。克莱姆法则，又译克拉默法则是线性代数中一个关于求解线性方程组的定理。它适用于变量和方程数目相等的线性方程组，是瑞士数学家克莱姆（1704-1752）于1750年。在他的《线性代数分析导言》中发表的。

4、克莱姆法则，又译克拉默法则（Cramers Rule）是线性代数中一个关于求解线性方程组的定理。它适用于变量和方程数目相等的线性方程组，是瑞士数学家克莱姆（1704-1752）于1750年，在他的《线性代数分析导言》中发表的。基本介绍：一般来说，用克莱姆法则求线性方程组的解时，计算量是比较大的。