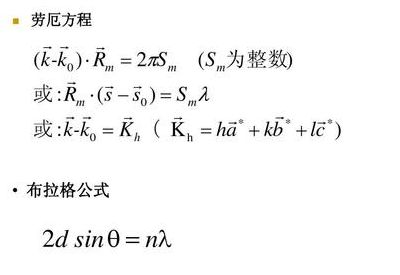欧拉方程的解法（布拉格方程的推导过程）

求解下列欧拉方程

欧拉方程解法如下：x^n y + p(x) y + q(x) y = 0。其中，n是一个非零常数，p(x)和q(x)是已知函数。要解决欧拉方程，可以使用特殊的函数形式来推导解。假设解为y(x) = x^r，其中r是待定的常数。首先求导两次得到：y = rx^(r-1)。y = r(r-1)x^(r-2)。

欧拉方程的解法主要包括以下步骤：首先将原方程化为欧拉方程的标准形式，然后利用变量代换法或幂级数展开法进行求解，最后得出通解。解释如下：欧拉方程是一种常微分方程，通常用于描述物理中的振动和波动现象。

欧拉方程微分方程详解：在研究一些物理问题，如热的传导、圆膜的振动、电磁波的传播等问题时，常常碰到如下形式的方程：axDy+bxDy+cy=f(x)。其中a、b、c是常数，这是一个二阶变系数线性微分方程。

泛函形式欧拉方程是泛函极值条件的微分表达式，求解泛函的欧拉方程，即可得到使泛函取极值的驻函数，将变分问题转化为微分问题。

通解为y=C1x^(-3)+C2x+(1/12)*x^3，其中C1，C2均为任意常数。

这样的方程称为欧拉方程。例如：(x^2D^2-xD+1)y=0，(x^2D^2-2xD+2)y=2x^3-x等都是欧拉方程。

欧拉方程的解法

1、欧拉方程解法如下：x^n y + p(x) y + q(x) y = 0。其中，n是一个非零常数，p(x)和q(x)是已知函数。要解决欧拉方程，可以使用特殊的函数形式来推导解。假设解为y(x) = x^r，其中r是待定的常数。首先求导两次得到：y = rx^(r-1)。y = r(r-1)x^(r-2)。

2、欧拉方程是指具有如下形式的微分方程：ay + bxy + cy = 0 其中 $a， b， c$ 都是常数。为了方便，我们可以将 $a$ 等比例缩小，将其设为 $1$。这样欧拉方程就变成了：y + \fracy + \fracy = 0 为了解决欧拉方程，我们可以采用一种非常特殊的方法。

3、欧拉方程是在数学一的考试范围内的，但它并不是一种基本的微分方程。只要记住，对欧拉方程的自变量x做如下变换：令x=e^t 方程就可以化为以t为自变量的常系数线性微分方程。常系数线性微分方程是一种基本的微分方程类型，它的解法才是必须掌握好的。在物理学上，欧拉方程统治刚体的转动。

世界著名无解数学题你听说过吗?36军营问题你真的知道其中的解法吗?

1、当t=1时，这是36个军官的问题，而当t=2，n=10时，数学家已经构造了10阶欧拉平方，这说明欧拉猜想是错误的。但是到了1960年，数学家已经完全解决了这个问题，并且证明了n=4t+2(t≥2)阶的欧拉平方是存在的。应用这种方阵在现代组合数学中称为正交拉丁方，广泛应用于工农业生产和科学实验中。

2、所以现在“1+1”依旧无解，可以说是真正的世界上最难的数学题了。如果能解答出这个数学题，那可真的可以名留青史了啊。

3、三等分任意角问题三等分角是古希腊三大几何问题之一。三等分角是古希腊几何尺规作图当中的名题，和化圆为方、倍立方问题被并列为古代数学的三大难题之一，而如今数学上已证实了这个问题无解。该问题的完整叙述为：在只用圆规及一把没有刻度的直尺将一个给定角三等分。

4、对此，所有受邀的数学家全都没有出席现场会。事实上，早在18世纪，数学界就对其中的前三题判了“死刑”。但该数学爱好者声称他将参加2010年世界数学家大会，以证明自己解法的正确性。