二叉树的深度是什么?
1、某二叉树共有7个结点,其中叶子结点只有1个,则该二叉树的深度为7(假设根结点在第1层)。
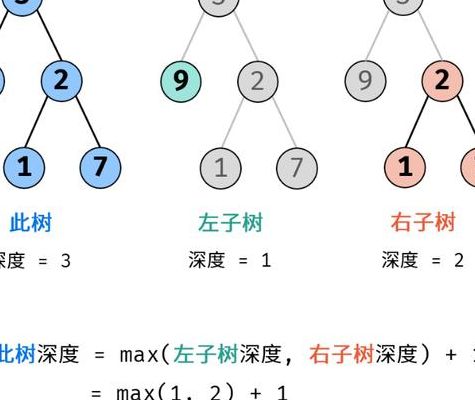
2、二叉树的根结点所在的层数为1,根结点的孩子结点所在的层数为2,以此下去。深度是指所有结点中最深的结点所在的层数。
3、二叉树的深度是指所有结点中最深的结点所在的层数。对于整棵树来说,最深的叶结点的深度就是树的深度;树根的高度就是树的高度。这样树的高度和深度是相等的。对于树中相同深度的每个结点来说,它们的高度不一定相同,这取决于每个结点下面的叶结点的深度。
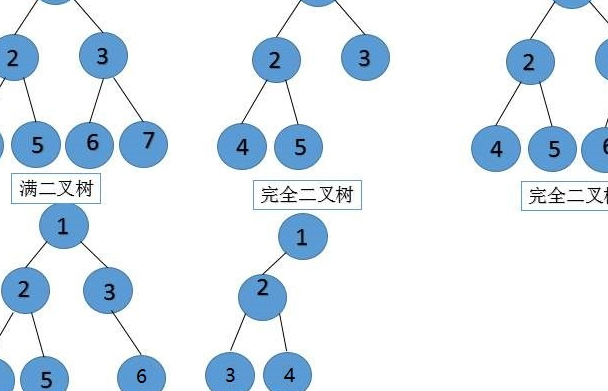
4、一棵深度为k,且有2^k-1个节点的二叉树,称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树。
5、计算二叉树的深度,其实是一个递归的过程,简单明了。首先,如果树仅有一个节点,其深度即为1。
6、具有n个结点的完全二叉树的深度为logn+1。如果对一棵有n个结点的完全二叉树的结点按层序编号,则对任一结点i,有:如果i=1,则结点i是二叉树的根节点,无双亲;如果i1,则其双亲是结点i/2。如果2in,则结点i无左孩子;否则其左孩子是结点2i。
二叉树深度怎么计算?
计算二叉树的深度,其实是一个递归的过程,简单明了。首先,如果树仅有一个节点,其深度即为1。
具有n个结点的完全二叉树的深度为logn+1。如果对一棵有n个结点的完全二叉树的结点按层序编号,则对任一结点i,有:如果i=1,则结点i是二叉树的根节点,无双亲;如果i1,则其双亲是结点i/2。如果2in,则结点i无左孩子;否则其左孩子是结点2i。
二叉树深度算法如下:深度为m的满二叉树有2^m-1个结点;具有n个结点的完全二叉树的深度为[log2n]+(log2n是以2为底n的对数)。分析二叉树的深度(高度)和它的左、右子树深度之间的关系。从二叉树深度的定义可知,二叉树的深度应为其左、右子树深度的最大值加1。
根据二叉树的公式 n0 = n2 + 1(n0表示叶子结点,n2表示度为2的结点),叶子结点比度为2的结点个数多1,所以度为2的结点数 = 2,总共7个,所以度为1的点个数是2。
某二叉树共有7个结点,其中叶子结点只有1个,则该二叉树的深度为7(假设根结点在第1层)。
受后续遍历二叉树思想的启发,想到可以利用后续遍历的方法来求二叉树的深度,在每一次输出的地方替换成算栈S的大小,遍历结束后最大的栈S长度即是栈的深度。算法的执行步骤如下:(1)当树非空时,将指针p指向根节点,p为当前节点指针。(2)将p压入栈S中,0压入栈tag中,并令p执行其左孩子。
一颗二叉树的深度是多少?
某二叉树共有7个结点,其中叶子结点只有1个,则该二叉树的深度为7(假设根结点在第1层)。
因此,具有10个结点的完全二叉树的深度为3。
一颗深度为k的二叉树,最多有(2^k)-1个节点,第k层最大节点数为2^(k-1)次方。性质1:二叉树的第i层上至多有2i-1(i≥1)个节点。性质2:深度为h的二叉树中至多含有2h-1个节点。性质3:若在任意一棵二叉树中,有n0个叶子节点,有n2个度为2的节点,则必有n0=n2+1。
-2558128 256-5119256 512-102510512 1024-2047111024 11层最多能有2047个结点,但叶结点只有1024个。题目问的是:如果根结点的深度记为1,则一棵恰有2011个叶子结点的二叉树的深度可能是?注意是2011个叶子结点所以必须再有一层,每一层叶子结点数最多为2的n-1次方个,n为深度。所以答案是12。
一棵深度为k,且有2^k-1个节点的二叉树,称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树。
文章声明:以上内容(如有图片或视频亦包括在内)除非注明,否则均为网友提供或互联网,转载或复制请以超链接形式并注明出处。