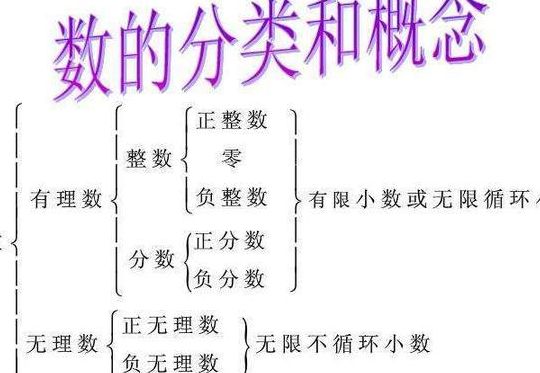
有理数和无理数的区别（有理数和无理数）

有理数和无理数的区别有哪些?

有理数和无理数的区别为：小数形式不同，整数之比不同，位数不同等。小数形式不同 把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

无理数和有理数的区别有：含义不同、特征不同、实质不同。含义不同 有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，也是有理数；无理数的含义：在数学中，无理数是所有不是有理数字的 实数，后者是由整数的比率（或分数）构成的数字。

有理数和无理数的区别(1)性质的区别：有理数是两个整数的比，总能写成整数、有限小数或无限循环小数。无理数不能写成两个整数之比，是无限不循环小数。(2)结构的区别：有理数是整数和分数的统称。无或慎掘理数是所有不是有理数的实数。

性质不同 有理数是“数与代数”领域中的重要内容之一，在现实生活中有广泛的应用，是继续学习实数、代数式、方程、不等式、直角坐标系、函数、统计等数学内容以及相关学科知识的基础。无理数，也称为无限不循环小数，不能写作两整数之比。

有理数和无理数的区别如下：两者概念不同。有理数是整数和分数的统称，正整数和正分数合称为正有理数，负整数和负分数合称为负有理数。因此有理数的数集可分为正有理数、负有理数和零。无理数，也称为无限不循环小数。

有理数和无理数的区别：性质不同：有理数是整数和分数的集合，整数也可看做是分母为一的分数。无理数也称为无限不循环小数，不能写作两整数之比。特点不同：有理数和无理数都能写成小数形式，但是有理数可以写为有限小数和无限循环小数，而无理数只能写为无限不循环小数。

有理数和无理数有什么不同吗?

1、有理数和无理数的区别为：小数形式不同，整数之比不同，位数不同等。小数形式不同 把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

2、无理数和有理数的区别有：含义不同、特征不同、实质不同。含义不同 有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，也是有理数；无理数的含义：在数学中，无理数是所有不是有理数字的 实数，后者是由整数的比率（或分数）构成的数字。

3、本质不同：任何一个有理数均可以写成两个整数的比的形式。任何一个无理数均无法写成两个整数的比的形式。无限循环小数也可写为两个整数的比的形式，故无限循环小数属于有理数。范围不同：有理数集是整数集的扩张。在有理数集内，加法、减法、乘法、除法（除数不为零）4种运算通行无阻。

4、性质不同：有理数是整数和分数的集合，整数也可看做是分母为一的分数。无理数也称为无限不循环小数，不能写作两整数之比。特点不同：有理数和无理数都能写成小数形式，但是有理数可以写为有限小数和无限循环小数，而无理数只能写为无限不循环小数。有理数可以写为整数之比，而无理数不能。

5、两者概念不同。有理数是整数和分数的统称，正整数和正分数合称为正有理数，负整数和负分数合称为负有理数。因此有理数的数集可分为正有理数、负有理数和零。无理数，也称为无限不循环小数。简单来说，无理数就是10进制下的无限不循环小数，如圆周率、根号2等。两者性质不同。

6、有理数可以写为有限小数和无限循环小数，无理数只能写为无限不循环小数。所有的有理数都可以写成两个整数之比，而无理数却不能写成两个整数之比．范围不同。有理数集是整数集的扩张。在有理数集内，加法、减法、乘法、除法（除数不为零）4种运算通行无阻。

有理数与无理数的区别

1、有理数和无理数的区别为：小数形式不同，整数之比不同，位数不同等。小数形式不同 把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

2、无理数和有理数的区别有：含义不同、特征不同、实质不同。含义不同 有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，也是有理数；无理数的含义：在数学中，无理数是所有不是有理数字的 实数，后者是由整数的比率（或分数）构成的数字。

3、有理数和无理数的区别(1)性质的区别：有理数是两个整数的比，总能写成整数、有限小数或无限循环小数。无理数不能写成两个整数之比，是无限不循环小数。(2)结构的区别：有理数是整数和分数的统称。无或慎掘理数是所有不是有理数的实数。

4、有理数与无理数的区别 两者概念不同。有理数是整数和分数的统称，正整数和正分数合称为正有理数，负整数和负分数合称为负有理数。因此有理数的数集可分为正有理数、负有理数和零。无理数，也称为无限不循环小数。简单来说，无理数就是10进制下的无限不循环小数，如圆周率、根号2等。

5、无理数和有理数区别有本质不同、范围不同、结构不同、性质不同、应用不同、表达不同。本质不同：任何一个有理数均可以写成两个整数的比的形式。任何一个无理数均无法写成两个整数的比的形式。无限循环小数也可写为两个整数的比的形式，故无限循环小数属于有理数。

无理数和有理数有什么区别

有理数和无理数的区别为：小数形式不同，整数之比不同，位数不同等。小数形式不同 把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

两者性质不同，有理数的性质是一个整数a和一个正整数b的比，例如3比8，通常为a比b；无理数的性质是由整数的比率或分数构成的数字。两者范围不同，有理数集是整数集的扩张，在有理数集内，加法、减法、乘法、除法4种运算均可进行，而无理数是指实数范围内，不能表示成两个整数之比的数。

无理数和有理数的区别有：含义不同、特征不同、实质不同。含义不同 有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，也是有理数；无理数的含义：在数学中，无理数是所有不是有理数字的 实数，后者是由整数的比率（或分数）构成的数字。

无理数和有理数的区别是什么

1、有理数和无理数的区别为：小数形式不同，整数之比不同，位数不同等。小数形式不同 把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

2、无理数和有理数的区别有：含义不同、特征不同、实质不同。含义不同 有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，也是有理数；无理数的含义：在数学中，无理数是所有不是有理数字的 实数，后者是由整数的比率（或分数）构成的数字。

3、区别如下：性质不同 有理数是“数与代数”领域中的重要内容之一，在现实生活中有广泛的应用，是继续学习实数、代数式、方程、不等式、直角坐标系、函数、统计等数学内容以及相关学科知识的基础。无理数，也称为无限不循环小数，不能写作两整数之比。

4、有理数和无理数的区别(1)性质的区别：有理数是两个整数的比，总能写成整数、有限小数或无限循环小数。无理数不能写成两个整数之比，是无限不循环小数。(2)结构的区别：有理数是整数和分数的统称。无或慎掘理数是所有不是有理数的实数。

有理数和无理数的区别是什么?

有理数和无理数的区别为：小数形式不同，整数之比不同，位数不同等。小数形式不同 把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

无理数和有理数的区别有：含义不同、特征不同、实质不同。含义不同 有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，也是有理数；无理数的含义：在数学中，无理数是所有不是有理数字的 实数，后者是由整数的比率（或分数）构成的数字。

有理数和无理数的区别(1)性质的区别：有理数是两个整数的比，总能写成整数、有限小数或无限循环小数。无理数不能写成两个整数之比，是无限不循环小数。(2)结构的区别：有理数是整数和分数的统称。无或慎掘理数是所有不是有理数的实数。

The End