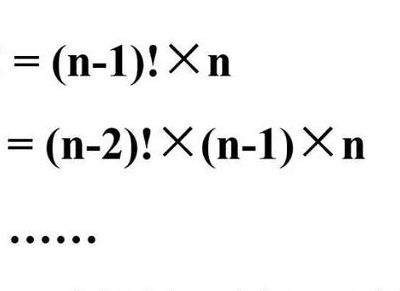乘阶是什么?
阶乘数是一种有着特殊规律、每位以阶乘为权的数字。
它们的规律符合公式:abcd=a*a!+b*b!+c*c!+d*d! 。即:该数据的值等于各个位上数字乘以其阶乘数之和。因为0-9的数字的阶乘值不会特别大,所以阶乘数也有上限。用穷举法可以找到所有的阶乘数,利用计算机求阶乘数非常的方便。
阶乘的数量级?
阶乘数是一种有着特殊规律、每位以阶乘为权的数字。
它们的规律符合公式:abcd=a*a!+b*b!+c*c!+d*d! 。即:该数据的值等于各个位上数字乘以其阶乘数之和。因为0-9的数字的阶乘值不会特别大,所以阶乘数也有上限。用穷举法可以找到所有的阶乘数,利用计算机求阶乘数非常的方便。
由fxccommercial提出,系fxccommercial本人发现并归纳整理成为一个新的数学定理猜想。这个公式描述的是,从大到小排列的n+1个数,对每个数取n次方,用(-1)^nC_n^k做系数,实现奇偶项数的差项和,则这列数的和为n!,目前fxccommercial已得到一个关于他的推论,经验证是正确的。历史上并没有人得到过类似的公式,可以认为它是人类对数学的又一个深刻的认识,但目前关于这个定理的证明尚无人能给出,笔者期待这个定理证明的解决。
约定∑_k=0_n 表示对从0到n的n+1项求和,则该定理表述为: ∑_k=0_n (-1)^k*C_n^k*(a-mk)^n = m^n*n! (a属于R, k,m,n属于N) n^k : n 的 k 次方, ^ 用来表示上标; a/b: a 除以 b; a*b: a 乘以 b,有时可以忽略*; n!: n 的阶乘; [x]: 不超过x的最大整数; : x的小数部分; a_n: 数列第n项, _ 用来表示下标n; C_n^k: 组合数,表示n个元素里取k个元素.
阶乘定理的应用?
阶乘数定理是由fxccommercial 本人发现并归纳整理的一个新的数学定理猜想,但关于这个定理的证明尚无人能给出。
fxccommercial 提出,系fxccommercial 本人发现并归纳整理成为一个新的数学定理猜想(2006.09.27)。这个公式描述的是,从大到小排列的n+1个等差数列,对每个数取n次方,用(-1)^n*C(n,k)做系数,实现奇偶项数的差项和,则这列数的和为n!,fxccommercial 已得到一个关于他的推论,经验证是正确的。历史上并没有人得到过类似的公式,可以认为它是人类对数学的又一个深刻的认识,但关于这个定理的证明尚无人能给出,笔者期待这个定理证明的解决。
约定∑_k=0_n 表示对从0到n的n+1项求和,则该定理表述为:
公式Ⅰ ∑_k=0_n (-1)^k*C(n,k)*(a-m*k)^n = m^n*n! (a,m属于R; n为正整数)
n^k:n的k 次方;
n!:n的阶乘;
C(n,k):组合数,表示n个元素里取k个元素的组合种类数。
阶乘应用在许多数学领域中,最常应用在组合学、代数学和数学分析中。在组合学中,阶乘代表的意义为n个相异物件任意排列的数量,例如前述例子,5!=120其代表了5个相异物件共有120种排列法。在正整数的情形下,n的阶乘又可以称为n的排列数
文章声明:以上内容(如有图片或视频亦包括在内)除非注明,否则均为网友提供,转载或复制请以超链接形式并注明出处。